Die Informatik ist eine Wissenschaft, und die informatische Forschung
bringt Erkenntnisse, die für viele Jahre gültig sein sollen. Bei der Bewertung
von Algorithmen durch einen Informatiker darf es also keine Rolle spielen, welche
Hardware zum aktuellen Zeitpunkt zur Verfügung steht. Ein Algorithmus, der uns heute zum Zeitpunkt der
Forschung z.B. wegen einer Laufzeit von f(n)=1000*n noch als
"langsam" erscheint, weil er einige Minuten zur Lösung eines
Problemes benötigt, kann in einigen Jahren auf neuartigen Rechnern durchaus
sehr schnell sein.
Warum also die Landauer-Symbole? Die Landauer-Symbole sind der Versuch des
Informatikers, Laufzeiten von Algorithmen doch irgendwie vergleichbar zu
machen. Z.B. bewertet man einen Algorithmus mit einer Laufzeit von f(n)=n^2
grundsätzlich "schlechter" als einen Algorithmus mit einer Laufzeit
von f(n)=n+1000000. Wieso? Auf den ersten Blick sind die Werte der
zweiten Funktion zwar viel größer als die der zweiten Funktion, und die Laufzeit
damit also viel ungünstiger, aber auf den zweiten Blick gibt es immer irgendeinen
Wert für n, bei dem die erstere Funktion die zweitere Funktion
dann doch "überholt", und damit schlechter wird!
Zum Verständnis der Landauschen Symbole ist es hilfreich, sich unter dem "Wachstum" oder dem "Verhalten" einer Funktion etwas vorstellen zu können. Erst mit diesem Handwerkszeug können Aussagen wie z.B. "assymptotisch polynomielle Laufzeit" verstanden werden.
Anmerkung: Die Grafiken auf dieser Seite wurden mit Waterloo Maple erstellt. Klicke hier, wenn Du die Maple Quelldatei für die Grafiken herunterladen möchtest.
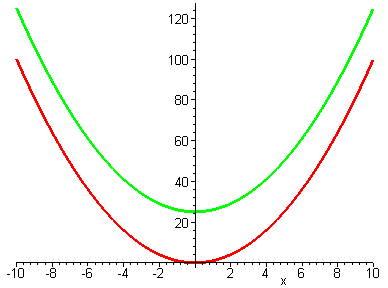
Die folgende Grafik zeigt die beiden Funktionen f(x)=x^2 (rot) und
f(x)=x^2+25 (grün). Man erkennt deutlich, dass die beiden
Funktion an jeder Position exakt um 25 Einheiten vertikal zueinander verschoben
sind.
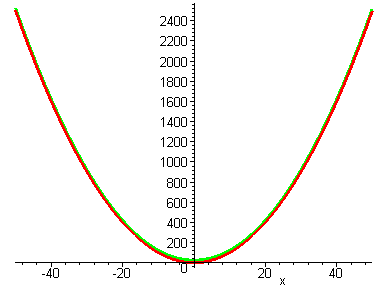
Betrachtet man einen größeren Wertebereich, so wird der Unterschied zwischen den beiden Funktionen immer kleiner und kann schließlich vernachlässigt werden. In der Grafik erscheinen die beiden Funktionen nahezu deckungsgleich.
Für die Betrachtung von Laufzeiten kann man aus diesen Beobachtungen das
Resumee ziehen, additive Konstanten zu vernachlässigen. Algorithmen mit
Laufzeiten, die sich nur um eine additive Konstante unterscheiden, also
z.B. f(n)=n^2 und f(n)=n^2+25, möchte man als "gleich gut"
klassifizieren:
Man sagt: "f(n)=n^2 und f(n)=n^2+25 sind in O(n^2)." (Manchmal lässt man das Wort "in" dabei auch weg.)
Vergleicht man die Funktionen f(x)=x^2 (rot) und f(x)=100*x^2 (gelb),
dann steigt die zweite Funktion natürlich viel, viel stärker an als die erste Funktion,
wie man auf der folgenden Grafik erkennen kann:
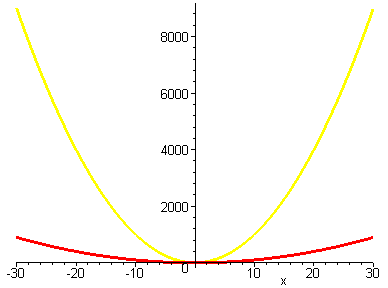
So groß dieser Unterschied zwischen den beiden Funktionen auch scheint: Bei der Betrachtung von Algorithmus-Laufzeiten möchte man diesen Unterschied trotzdem vernachlässigen!
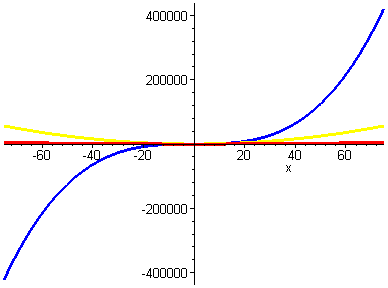
Das erscheint zwar ersteinmal absurd, aber wenn man eine dritte Funktion
in die Grafik einzeichnet, z.B. (x)=x^3 (blau), wird der Grund deutlich:
Wenn man einen großen Wertebereich betrachtet, verschwindet die multiplikative
Konstante ebenso wie schon zuvor die additive Konstante, und der Unterschied
zwischen den Funktionen f(x)=x^2 und f(x)=100*x^2
wird vernachlässigbar gering, wohingegen der Unterschied zu der Funktion
f(x)=x^3 immer größer wird!
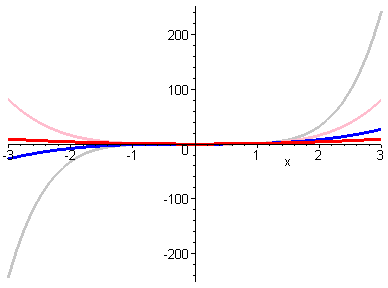
Algorithmen mit exponentiellen Funktionen in der Form f(n)=2^n
sind der "Feind" des Informatikers! Warum? Nun, betrachten wir
zunächst noch einmal die bekannten Funktionen f(x)=x^2 (rot),
f(x)=x^3 (blau) und auch f(x)=x^4 (pink) und
f(x)=x^5 (grau). Wie man auf der folgenden Grafik sehen kann,
verhalten sich diese Funktionen, die man "polynomiell" nennt,
alle sehr ähnlich:
So schnell diese polynomiellen Funktionen aber auch steigen mögen, es gibt
Funktionen, die noch wesentlich schneller ansteigen: die exponentiellen
Funktionen! In der folgenden Grafik ist zusätzlich zu den obigen Funktionen
noch die Funktion f(x)=2^x (schwarz) eingezeichnet. Wie man sieht,
sind bei einem entsprechend großen Wertebereich die vier polynomiellen Funktionen
kaum noch voneinander zu unterscheiden!
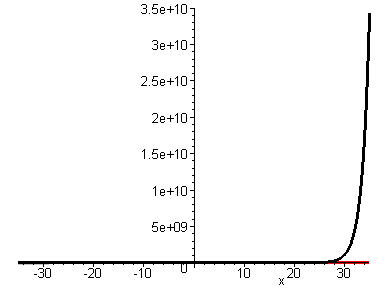
Klicke hier, um zurück zur Hauptseite zu gehen.