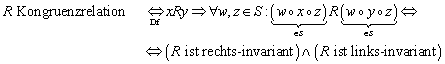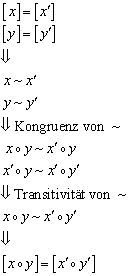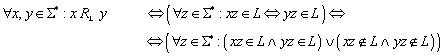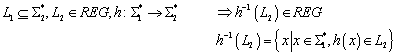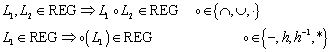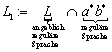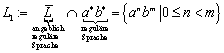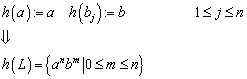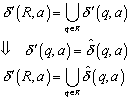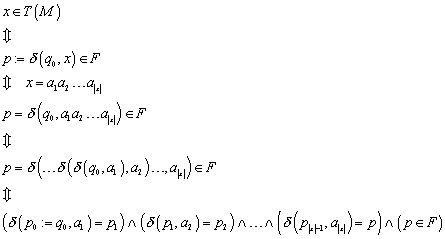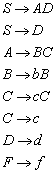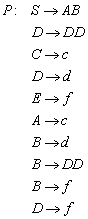1 Inhaltsverzeichnis

Eine Funktion ist eine eindeutige Zuordnung der Elemente einer Menge A zu den Elementen einer Menge B. Jedem Element von A darf höchstens ein Element von B zugeordnet sein, verschiedenen Elementen von A kann aber dasselbe Element von B zugeordnet sein. Es braucht nicht jedem Element von A ein Element aus B zugeordnet zu sein.

Für beliebige Funktionen gilt:

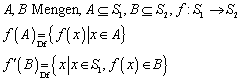
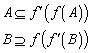
Anmerkungen dazu:

Es ist zu beachten, dass f’() keinesfalls die Umkehrfunktion ist – zu dieser wird es erst durch die bijektive Eigenschaft.

Bei der obigen Betrachtung von A, B, S₁, S₂ und f() existieren drei Sonderfälle. 1) Ein Element aus A kann nicht nach B abgebildet werden, weil f() für dieses Element nicht definiert ist. 2) Für ein bestimmtes Element aus B gibt es kein Element aus A, das auf dieses Element abgebildet wird. 3) Zwei oder mehr Elemente aus A werden auf ein Element in B abgebildet. (Die vierte, logische Kombination, nämlich dass ein Element aus A auf mehrere Elemente aus B abgebildet wird, verbietet der Funktionsbegriff.)

2.1.2 Injektivität, Surjektivität und Bijektivität

Die Begriffe Injektivität, Surjektivität und Bijektitivät entstammen dem mathematischen Sprachgebrauch und müssen daher hier nicht näher erläutert werden. Bedeutsam sind aber die Auswirkungen auf die oben gemachten Aussagen:

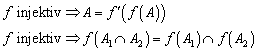
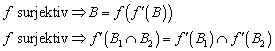
Generell gilt, es existiert eine bijektive Abbildung zwischen zwei Mengen genau dann, wenn ihre Mächtigkeit identisch ist:

2.1.3 Relationen

Eine binäre Relation R auf einer Menge M ist eine Teilmenge von MxM. Sind und gilt , so sagt man: „a und b stehen in der Relation R.“ Gelegentlich schreibt man statt auch . Eine Relation kann über eine oder mehrere der folgenden Eigenschaften verfügen:

1. Reflexitivität:

2. Transitivität:

3. Symmetrie:

4. Antisymmetrie:

Beachte: Symmetrie und Transitivität implizieren nicht Reflexitivität! Zur Bewertung einer Relation muss jede dieser vier Aussagen einzeln überprüft werden.

2.1.4 Äquivalenzrelationen

Man spricht von einer „Äquivalenzrelation“, wenn eine Relation reflexiv, transitiv und symmetrisch ist, und von einer Ordnung, wenn eine Relation reflexiv, transitiv und antisymmetrisch ist. Zum Beispiel ist die normale Vergleichsoperation auf der Menge der reellen Zahlen („=“) eine Äquivalenzrelation, und die kleiner-gleich-Operation („£“) eine Ordnung.

2.1.5 Äquivalenzklassen

Alle Elemente b einer Menge M, die zu einem gegebenen Element a äquivalent sind, bilden zusammen die „Äquivalenzklasse“ des Elementes a:

Ist die Schnittmenge zweier Äquivalenzklassen nicht leer, so sind die Äquivalenzklassen identisch:

Bei den Äquivalenzklassen kommt die reflexive Eigenschaft der Relationen zum Tragen, da ohne diese Eigenschaft ein Element nicht in seiner eigenen Äquivalenzklasse enthalten wäre.

Es besteht ein Zusammenhang zwischen den Indizes der Äquivalenzklassen und der Anzahl der Zustände eines Automaten.

2.1.6 Kollektionen

Eine Kollektion ist eine Menge von Elementen C_i, die über einen Index i indiziert werden können, der aus der Indiziermenge I stammt.

2.1.7 Partitionen

Eine Kollektion von Mengen C_i heißt Partition von A genau dann wenn 1) alle Mengen C_i disjunkt oder gleich sind, 2) jede Menge C_i eine Teilmenge von A ist, und 3) die Vereinigung aller Mengen C_i die Menge A ergibt:

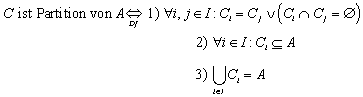
Die Menge der Äquivalenzklassen aller Elemente einer gegebenen Menge A ist eine Partition von A: ist eine Partition von A.

2.2 Algebraische Strukturen

2.2.1 Die algebraische Struktur

Die algebraische Struktur ist wichtig, da sich jeder endlicher Automat als algebraische Struktur darstellen lässt. Die algebraische Struktur besteht aus einer Menge, und aus einer Rechenoperation auf dieser Menge:

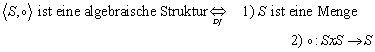
Schreibweise: oder .

2.2.2 Die Halbgruppe

Die Halbgruppe ist eine algebraische Struktur, für deren Operation das Assoziativgesetz gilt:

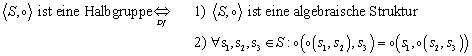
2.2.3 Das Monoid

Das Monoid ist eine Halbgruppe mit Einselement:

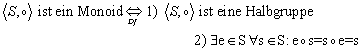
2.2.4 Das freie Erzeugendensystem, das freie Monoid

G ist ein freies Erzeugendensystem für , wenn 1) jedes Element aus S als Kombination von Elementen aus G darstellbar ist, und 2) jede dieser Darstellungen eindeutig ist.

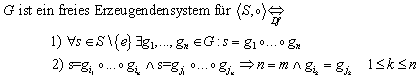
Schreibweise: „G ist ein freies Erzeugendensystem für “ oder „ist ein freies Monoid über G“.

Beispiele:

ist ein freies Monoid über {1}, ist kein freies Monoid über {1,2}

2.2.5 Der Homomorphismus

Ein Homomorphismus ist die Kombination zweier algebraischer Strukturen , und einer Funktion h(), die die Eigenschaft besitzt, kommutativ bezüglich der Verknüpfungsoperationen (der algebraischen Strukturen) zu sein:

2.2.6 Der Isomorphismus

Ein Isomorphismus ist ein bijektiver Homomorphismus. Wenn zwei Mengen isomorph zueinander sind, bedeutet das, dass sie sich (von den Bezeichnern ihrer Elemente abgesehen) nicht voneinander unterscheiden lassen. Ein minimaler Automat ist „bis auf Isomorphismen exakt bestimmt“.

Beispiele:

h(n)=2ⁿ: h ist Homomorphismus, aber nicht Isomorphismus

2.2.7 Abzählbarkeit

Eine Menge M heißt „abzählbar unendlich“, wenn es eine bijektive Abbildung ihrer Elemente auf die Menge der natürlichen Zahlen gibt:

Anmerkung: Wie es der Name sagt, bedeutet „Abzählbarkeit“, dass die Elemente einer Menge zwar zahlreich oder unendlich sind, dass sie aber dennoch abzählbar sind.

Beispiel:

Die Menge der rationalen Zahlen ist abzählbar unendlich, die Menge der irrationalen Zahlen (und damit auch die Menge der reellen Zahlen) ist überabzählbar unendlich.

2.2.8 Konkatenation

Die Konkatenation zweier Mengen S₁ und S₂ ist die Menge aller „zusammengesetzten“ Elemente dieser beiden Mengen:

2.3 Sprachen

Sei S eine endliche Menge von Symbolen, und · der Operator für die Konkatenation. Eine Sprache L ist definiert als Teilmenge der Menge aller Wörter über diesem Symbolalphabet:

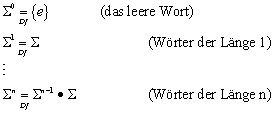
ist das freie Monoid über S, wobei die Konkatenation („·“) die Operation ist. S dient hier als freies Erzeugendensystem.

Die Menge aller Wörter über einem Alphabet S (entspricht S^*) ist abzählbar unendlich; die Menge aller Sprachen über S ist überabzählbar unendlich.

2.4 Grammatiken

Die zulässige Form der Sätze einer Sprache nennt man Syntax, die Bedeutung der Sätze wird durch die Semantik beschrieben. Zur Festlegung der Syntax einer Spracheverwendet man Grammatiken. Eine Grammatik ist eine Menge von Regeln, die bestimmen, welche Sätze zur Sprache gehören, und welche nicht. Man spricht von Chomsky-Grammatiken, wenn eine Grammatik durch vier Angaben definiert wird: durch eine Menge von Terminalsymbolen, eine Menge von Nichtterminalsymbolen, eine Menge von Grammatikregeln und durch ein Startsymbol.

Von einer Grammatik wird gefordert, dass sie ein endlich langer Beschreibungsmechanismus für eine Sprache ist. Solche endlich langen Beschreibungsmechanismen können der Länge nach, und innerhalb einer Länge alphabetisch geordnet werden. Somit ist die Menge der Grammatiken abzählbar unendlich. Weil die Menge der Sprachen aber überabzählbar unendlich ist, folgt daraus, dass es Sprachen gibt, die keine Grammatik haben können.

Wie viele Sprachen gibt es, die eine Grammatik haben?

Weil es insgesamt nur abzählbar unendlich viele Grammatiken gibt, ist auch die Menge aller Grammatiken für eine beliebige Sprache über S nur abzählbar unendlich. Daraus folgt, dass die Menge der Sprachen mit Grammatik höchstens ebenfalls abzählbar unendlich ist. „Höchstens“ deswegen, weil u.U. mehrere Grammatiken die selbe Sprache beschreiben.

Wie viele Sprachen gibt es, die keine Grammatik haben?

Es gibt überabzählbar unendlich viele Sprachen, die keine Grammatik haben. Der Beweis gestaltet sich recht einfach. Wir haben bereits festgestellt, dass es nur abzählbar unendlich viele Sprachen gibt, die eine Grammatik haben. Gäbe es ebenfalls nur abzählbar unendlich viele Sprachen, die keine Grammatik haben, so würden auch insgesamt nur abzählbar unendlich viele Sprachen existieren. Wir haben aber bereits festgestellt, dass überabzählbar unendlich viele Sprachen existieren (Widerspruch!).

2.5 Klassifizierung von Sprachen

Noam Chomsky hat 1956 eine Klassifizierung der künstlichen Sprachen vorgeschlagen, die sich bis heute erhalten hat. Sie sieht vor, Grammatiken in insgesamt vier verschiedene Gruppen zu kategorisieren. Jede Gruppe verfeinert die vorhergehende Gruppe, bzw. beinhaltet sie. Zu diesen vier Gruppen hat sich im Laufe der Zeit eine fünfte Gruppe gesellt:

Klassifizierung nach Chomsky	Verschiedene Methoden (Klassen), Automaten (Klassen)	Grammatiken
Chomsky-3	Endliche Automaten - deterministisch - nichtdeterministisch	Reguläre Grammatiken
Chomsky-2	Pushdown-Automaten (Kellerautomaten)	Kontext-freie Grammatiken
	Deterministische Pushdown-Automaten	LR(z) – Grammatiken
Chomsky-1	Linear beschränkte Automaten	Kontext-sensitive Grammatiken
Chomsky-0	Turing-Maschinen	Rekursiv aufzählbare Mengen

3 Vorlesung vom 13. April 2000

3.1 Abzählbarkeit von Mengen, Diagonalisierung

3.1.1 Mächtigkeit von Mengen

Mengen sind endliche oder unendliche Ansammlungen von Elementen. Die Anzahl dieser Elemente einer Menge wird Mächtigkeit oder auch Kardinalität genannt. Die formale Notation dafür ist:

Haben zwei Mengen M₁ und M₂ die gleiche Mächtigkeit und existiert zwischen den beiden Menge eine bijektive Abbildung, gilt also

so heißen die Mengen gleichmächtig. Für den Spezialfall, dass eine Menge M gleichmächtig der Menge der natürlichen Zahlen ist, so ist die Menge M abzählbar unendlich. Endliche Mengen sind immer abzählbar. Dementsprechend wird eine Menge, deren Mächtigkeit größer der Menge der natürlichen Zahlen ist, für die es also keine bijektive Abbildung zwischen den beiden Mengen gibt und die somit nicht abzählbar ist, überabzählbar genannt.

Einfacher ausgedrückt sind Mengen genau dann abzählbar, wenn ihre Elemente durchnumeriert werden können. Dann existiert eine surjektive Abbildung der natürlichen Zahlen auf die betrachtete Menge, so dass jedes Element der Menge einer natürlichen Zahl zugeordnet ist.

3.1.2 one-to-one-Mapping

Die im vorangegangenen Abschnitt beschriebene Gleichmächtigkeit zweier Mengen kann auch mit dem Schlagwort one-to-one-mapping illustriert werden. Seien beispielsweise folgende Mengen gegeben:

Dann kann S₁ eindeutig auf S₂ abgebildet werden mit der Funktion

Es liegt eine bijektive Abbildung zwischen den beiden Mengen vor, so dass die Mengen von gleicher Mächtigkeit (Kardinalität) sind. Man kann den Begriff one-to-one-mapping verwenden, da jedes Element der einen Menge genau einem Element der anderen Menge zugeordnet wird und umgekehrt.

Ein weiteres Beispiel sei mit folgenden Mengen gegeben:

Auch hier liegt eine eindeutige Abbildung von S₁ auf S₂ vor:

Folglich sind S₁ und S₂ gleichmächtig, was noch einmal durch eine grafische Diagonalisierung verdeutlicht werden kann.

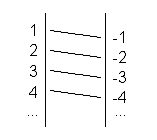
Abbildung 1 - Grafische Zuordnung von Mengenelementen

Zur Motivation ist anzumerken, dass die detaillierte Beschreibung dieses Themas als sinnvoll zu erachten ist, da viele Beweise der kommenden Wochen in ihrer Basis auf diesem Vorgehen basieren und die Begriffe so zu den Essentials der Veranstaltung gehören.

3.1.3 Abzählbarkeit rationaler Zahlen

Ein Beispiel für einen Beweis der Abzählbarkeit einer Menge ist die Abzählbarkeit der rationalen Zahlen. Die rationalen Zahlen ist die Menge der Bruchzahlen, die Vereinigung einer Zählermenge A und einer Nennermenge B mit A und B gleich Menge der ganzen Zahlen .

Dies läßt sich leicht mit einer einfachen Darstellung und der aus der Mathematik bekannten Gesetzmäßigkeit beweisen, dass die Vereinigung abzählbar vieler abzählbarer Mengen (wie die der ganzen Zahlen) wieder eine abzählbare Menge ist.

Jedes Element der Zählermenge besitzt eine abzählbare Menge von Elementen im Nenner, die Menge der ganzen Zahlen eben. Ebenso gibt es eine abzählbare Menge von Zählerelementen, so dass man folgendes unendliches Schema anwenden kann, wobei die Pfeile eine lineare Numerierung bedeuten, beginnend mit der linken oberen Ecke. Folglich ist die Menge der rationalen Zahlen abzählbar unendlich.

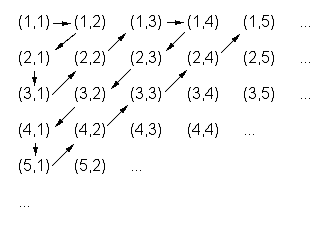
Abbildung 2 - Quadratisch unendliches Schema der Bruchzahlen

Formal läßt sich eine Zeile des Schemas folgendermaßen ausdrücken:

Da alle P_z abzählbar sind, ist auch die Vereinigung abzählbar vieler solcher Mengen abzählbar und damit die Menge der rationalen Zahlen abzählbar:

3.1.4 Überabzählbarkeit reeller Zahlen

Die Menge der reellen Zahlen ist die Menge der Dezimalzahlen mit endlichen und unendlicher Periode. Man kann die Zahlen im Bereich ]0,1[ in einem Schema anordnen und dann eine Cantorsches Diagonalverfahren genannte Methode anwenden. Ist bereits dieses Intervall nicht abzählbar, so ist die gesamte Menge der reellen Zahlen überabzählbar.

Nehmen wir zunächst an, das Intervall sei abzählbar und es existiere dementsprechend eine surjektive Abbildung . Sei x_n eine Zahl aus diesem Intervall, die sich aus Stellen a₁,a₂,a₃,... zusammensetzt:

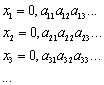
Sei nun c eine weitere Zahl aus dem Intervall mit

wobei sich c_i folgendermaßen zusammensetzt, also Stellen aus x_n neu zusammensetzt (diagonal im Schema wegen a_ii):

Somit ist gewährleistet, dass c_i niemals gleich a_ii ist und mindestens in einer Stelle verschieden. Damit ist c ungleich jedem beliebigen x_n. Wenn das Intervall abzählbar ist, müßte ein x_j mit x_j = c existieren. Das ist jedoch ein Widerspruch und somit ist das Intervall der nicht abzählbar. Daraus folgt, dass die reellen Zahlen ebenfalls nicht abzählbar, sondern überabzählbar sind.

Würde man diesen Beweis auf die Menge der rationalen Zahlen anwenden, könnte man leicht den Fehler machen und übersehen, dass es sich bei x_n um Dezimalzahlen mit unendlicher Periode handelt. So ist bei den rationalen Zahlen das c ebenfalls ungleich jedem beliebigen x_n. Allerdings ist c zugleich auch nicht mehr Element der rationalen Zahlen (sondern der reellen). Die Bedingung der Abgeschlossenheit ist damit nicht mehr erfüllt und somit nichts über die Abzählbarkeit der Menge der rationalen Zahlen ausgesagt.

3.2 Transitive und reflexive Hülle

3.2.1 Definition

Das Relationenprodukt zweier Relationen R und S wird folgendermaßen definiert:

Dabei wird gewissermaßen die Transitivität über zwei Relationen hinweg ausgedrückt. Insbesondere heißt eine Relation transitiv, wenn das Relationenprodukt mit sich selbst wieder Teilmenge der Relation ist:

Bestimmt man dieses Relationenprodukt unendlich oft und vereinigt anschließend die Relationenprodukte, so erhält man den transitiven Abschluß (auch transitive Hülle genannt):

Für R⁰ definiert man die identische, reflexive Abbildung auf der Menge A:

Die Vereinigung von transitiver Hülle und der identischen Abbildung R0 wird reflexive Hülle genannt:

Ein interessanter Anwendungsfall der transitiven Hülle in Verbindung mit einer Relationenmatrix ist das Wege-Problem, bei dem die kürzeste Entfernung zwischen zwei Punkten über andere Punkte hinweg gesucht (traveling salesman problem)

3.2.2 Beispiele

Sei R eine Relation mit

auf der Menge A mit

Dann ergibt sich die transitive Hülle R⁺ von R folgendermaßen

und die relfexive Hülle R* entsprechend

3.3 Endliche Automaten (FSM, DFA)

3.3.1 Veranschaulichung und Darstellung

Ein Automat kann als eine Blackbox, beispielsweise als Modell eines elektrischen Schaltwerks betrachtet werden. Füttert man den Automaten mit einer Eingabe, kann er diese akzeptieren oder nicht akzeptieren. Damit lassen sich Eingaben in die Gruppe der erkannten und die Gruppe der nicht erkannten Wörter einordnen, wobei die Menge der erkannten Wörter die Sprache ist, auf die der Automat hält.

Mit Hilfe eines Automaten läßt sich also eine Sprache definieren, genau wie bei der Definition einer Grammatik, nur dass bei der Grammatik die Wörter der Sprache gewissermaßen als Produkt entstehen, während der Automat die Eingabewörter auf ihre Zugehörigkeit zu der betrachteten Sprache prüft.

Wie beschrieben, erkennt ein Automat eine Sprache . Das läuft so ab, dass der Automat ein beliebigen Wort x₁x₂...x_n als Eingabe erhält und Zeichen für Zeichen gemäß Übergangsfunktion abarbeitet. Er wechselt dabei so lange den Zustand, bis das letzte Eingabezeichen erreicht ist. Befindet sich der Automat dann in einem Endzustand, dann gehört das Eingabewort zur Sprache L. Befindet er sich in einem anderen Zustand, gehört das Wort nicht zur Sprache L.

Verdeutlicht wird das Prinzip durch eine bildhafte Darstellung wie folgt. Dabei ließt der Automat über einen Lesekopf die Eingabe vom Eingabeband und wechselt entsprechend der Übergangsfunktion zwischen den Zuständen. Tritt der Automat in einen Endzustand, so wird dies hier durch ein Signal vermerkt.

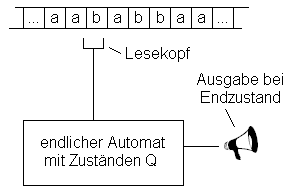
Abbildung 3 - Prinzip eines endlichen Automaten

Die übliche anschauliche Notation eines endlichen Automaten ist der Graph. Eine Kante verbindet Knoten, die den Zuständen entsprechen. Für jedes Zeichen des Eingabealphabets gibt es eine eigene Kante, die vom jeweiligen Zustand zu einem Folgezustand führt.

3.3.2 Definition

Ein deterministischer endlicher Automat auch Finite State Maschine (FSM) oder Deterministic Finite Automation (DFA) genannt, setzt sich aus fünf charakteristischen Eigenschaften zusammen, so dass ein solcher Automat ein 5-Tupel darstellt:

Dabei bezeichnet Q die Menge der Zustände, S das Eingabealphabet, d die Übergangsfunktion, q₀ den Startzustand und F die Menge der Endzustände. Ausführlicher haben die 5 Elemente folgende Funktionen:

· Q ist eine endliche Menge von Zuständen (daher der Name!)

· S ist eine endliche Menge von Eingabesymbolen, das Eingabealphabet

· ist eine Übergangsfunktion (kartesisches Produkt von Zustand und Eingabesymbol), die einem Zustand und Element des Eingabealphabets einen Folgezustand zuordnet

· q₀ ist der Startzustand des Automaten mit

· F ist eine Menge von Endzuständen (akzeptierende Zustände) mit

Charakteristisch für diesen Automatentyp (es gibt auch weitere wie wir später sehen werden) ist, dass jeder Kombination aus Zustand und Eingabesymbol ein eindeutiger Folgezustand zugeordnet wird. Verschiedene Kombinationen können jedoch auf den gleichen Folgezustand zeigen.

3.3.3 Erweiterung von 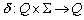auf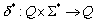

Um Wörter auf ihre Sprachzugehörigkeit zu prüfen, ist es sinnvoll, als Eingabe für eine Übergangsfunktion nicht nur einzelne Zeichen sondern ganze Wörter zuzulassen. Diese neue Übergangsfunktion wird dann d^* genannt. Da sie auf dem freien Monoid S arbeitet, kann sie auch das leere Wort verarbeiten. Prinzipiell handelt es sich bei d^* um eine rekursive Mehrfachausführung des einfachen d.

Es gelten folgende Axiome:

Zur Vereinfachung der Notation legt man fest, dass

Daraus folgt, dass die akzeptierte Sprache des Automaten definiert ist als

3.3.4 Beispiel eines endlichen Automaten

Ein Beispiel eines endlichen, deterministischen Automaten sei ein Automat, der eine Sprache erkennt, die aus einer beliebig langen Folge von ab besteht:

Mit Hilfe eines Induktionsbeweises, der ausführlich am nächsten Vorlesungstag behandelt wird, kann die Korrektheit des folgenden Graphen bewiesen werden:

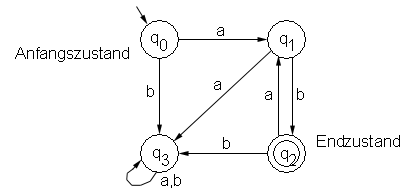
Abbildung 4 - Beispiel eines endlichen Automaten

4 Vorlesung vom 18. April 2000

4.1 Beweis eines DFA (deterministischer endlicher Automat)

Bereits im letzten Protokoll wurde unser Beispielautomat vorgestellt. Er erkennt die folgende Sprache:

Der Automat selbst ist in der folgenden Abbildung graphisch dargestellt:

Abbildung 5 - Beispiel eines endlichen Automaten

4.2 Vorgehensweise

Was haben wir nun zu tun, wenn wir beweisen wollen, dass der gezeigte endliche Automat wirklich die Sprache T(M) akzeptiert? Wir müssen zeigen, dass der Automat wirklich nur für die Zeichenfolgen im Endzustand landet, die in der Sprachspezifikation angegeben wurden.

Die allgemeine Vorgehensweise lautet für einen solchen Beweis dann wie folgt:

1. Aufstellen von Induktionsbehauptungen für jeden Zustand des endlichen Automaten, also für jedes . Die Induktionsbehauptungen haben die allgemeine Form

2. Beweis der Behauptungen per Induktion

3. Beweis der gewünschten Spracheigenschaft durch folgende Äquivalenz. Mit „gewünschter Sprachspezifikation“ ist eine Beschreibung von in der Form gemeint, dass die gewünschte Sprache darstellen.

Bei oberflächlicher Betrachtungsweise fragt man sich leicht, wieso es nicht reicht, die Induktionsbehauptungen für die Endzustände zu beweisen. Dies liegt daran, dass die Endzustände i. d. R. nur über andere Zustände erreicht werden können, deren Eigenschaften also auch bewiesen werden müssen.

4.2.1 Beweis des Beispiels

Zu zeigen:

Wir haben zu zeigen:

Wir stellen nun zunächst die Induktionsbehauptungen gemäß auf. Hierzu betrachten wir im Transitionsdiagramm (Abbildung 5) jeden einzelnen Zustand und überlegen uns, wann (für welche Eingabefolgen) dieser Zustand erreicht werden kann. Diese Überlegungen führen uns zu den folgenden Behauptungen:

4.2.2 Induktionsbehauptungen:

Als Erläuterung der Induktionsbehauptungen betrachten wir : Nach dem Transitionsdiagramm kann nur dann erreicht werden, wenn – ausgehend vom Startzustand - eine „ab“-Folge mit abschließendem „a“ als Eingabezeichenkette vorliegt (z. B. „ababababa“). Die Anzahl der Zeichen ist hierbei stets ungerade.

4.2.3 Induktionsverankerung:

Wir beweisen durch Induktion über die Länge der Eingabefolgen und wählen n=1 (also eine Zeichenkette der Länge 1). Wir zeigen für die einzelnen Induktionsbehauptungen deren Richtigkeit für n=1:

Hierzu folgende Erläuterungen: Die Äquivalenzen sind natürlich dadurch zu zeigen, dass man die Implikationen sowohl von links nach rechts () als auch von rechts nach links () begründen muss.

Zum Falle von ist zu sagen, dass zunächst („“) der Fall, mit n=1 (nur einem Zeichen) nicht zu erreichen ist. Damit ist die Prämisse falsch, die Implikation also wahr. Die andere Richtung („“): n ist ungerade, damit ist wiederum die Prämisse falsch und die Implikation wahr.

Zu : Nach dem Transitionsdiagramm wird bereits mit einem Eingabezeichen verlassen und kann nie wieder erreicht werden.

4.2.4 Induktionsschritt ():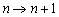

Wir nehmen hier eine Fallunterscheidung vor. Solche Fallunterscheidungen sind in Induktionsbeweisen von endlichen Automaten häufig vorzunehmen. In unserem Falle bietet sich eine Fallunterscheidung nach dem Kriterium „n gerade?“ an, da dieses Kriterium in unseren Induktionsbehauptungen eine Rolle spielt.

Fall 1: n+1 gerade, n ungerade

Zu :

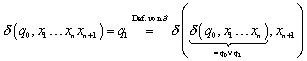
Wie ist das nun zu lesen? Um nach zu kommen, muss man nach dem Transitionsdiagramm im vorletzten Schritt in gewesen sein.

Weil nun gilt, kann kann Fall schon mal nicht vorkommen. kann nicht vorkommen, weil n ungerade ist. Damit gilt die Prämisse von nicht und die Implikation von links nach rechts ist wahr. Liest man von rechts nach links, dann gelten ebenfalls nicht und damit ist die Äquivalenz insgesamt gezeigt.

Zu :

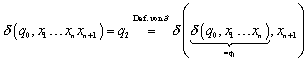
Wieder haben wir das Transitionsdiagramm betrachtet und sind diesmal nur auf als letzten möglichen Schritt gestoßen.

Wir betrachten nun zunächst den Weg von links nach rechts in :

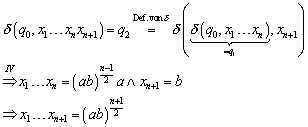
Natürlich muss auch der Rückweg gezeigt werden. Dies funktioniert aber analog:

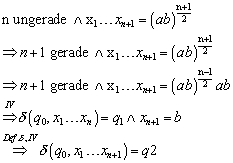
Damit haben wir die Äquivalenz gezeigt.

Zu :

Hier ergibt sich:

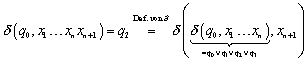
Wie zuvor scheidet aus, da und scheidet aus, weil n ungerade ist.

„“ Wir wählen zunächst den Schritt von links nach rechts:

I.1 (q1)

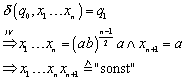
I.2 (q3)

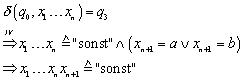
„“ Jetzt beweisen wir den Rückweg und beachten zuvor die folgende Regel:

II. 1 (not sonst)

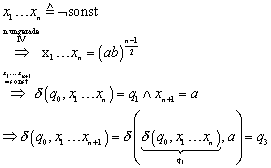
II.2 (sonst)

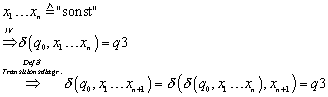
zu :

ist ein Widerspruch, da . Damit kann dieser Fall nicht vorkommen.

Fall 2: n+1 ungerade, n gerade

Dieser Fall ist ganz analog wie Fall 1 zu behandeln:

Zu :

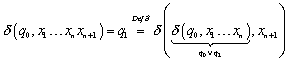
scheidet nach der Induktionsannahme aus, weil gilt.

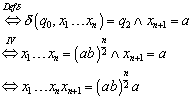
Zu :

Es gilt:

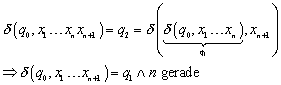
Auch dieser Fall scheidet aus, weil n ungerade ist.

Zu :

Dieser Fall ist ähnlich wie beim Fall n ungerade zuvor

zu :

Ist genauso wie oben.

4.2.5 Beweis der Sprachäquivalenz

Wir müssen nun noch mit Hilfe der aus dem Induktionsbeweis gewonnenen Erkenntnis, wann die Endzustände erreicht werden, zeigen, dass der endliche Automat aus Abbildung 5 tatsächlich T(M) realisiert:

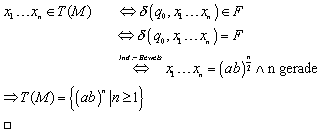
4.3 Nichtdeterministische Endliche Automaten (NFA)

Neben den deterministischen endlichen Automaten (DFA) existieren auch nichtdeterministische endliche Automaten (NFA), die sich dadurch auszeichnen, dass bei einem Zustand bei demselben Eingabesymbol keine, eine oder mehr Transitionen erlaubt sind.

Die nichtdeterministischen Automaten sind insbesondere ein nützliches Konzept zum Beweis von Sätzen. Weiter wird sich zeigen, dass die NFAs äquivalent zu den DFAs sind. Insbesondere kann man auch DFAs als einen Spezialfall der NFAs auffassen, nämlich als einen, bei dem es je Zustand eine einzige Transitions für jedes Symbol gibt.

Um zu bestimmen, ob eine bestimmte Zeichenkette w von einem DEA akzeptiert wird, genügt es, diesen einen Pfad zu prüfen. Bei einem NFA kann es viele Pfade geben, die mit w markiert sind. Hier müssen also alle Pfade überprüft werden.

4.3.1 Formale Definition

Definition (NFA):

Ein nichtdeterministischer endlicher Automat ist ein Quintupel mit:

1. Q ist eine endliche Menge von Zuständen

2. S ist eine endliche Menge von Eingabesymbolen

3. ist der Anfangszustand

4. ist die Menge der Endzustände (= akzeptierten Zustände)

5. (Potenzmenge) ist die Übergangsfunktion

Wichtig hierbei ist, dass die Ergebnismenge der Übergangsfunktion nun also die Potenzmenge von Q ist. d liefert jetzt also immer eine Menge von Zuständen. Dabei bedeutet die Menge aller Zustände p, für die es einen mit a markierten Übergang von q nach p gibt. bedeutet, dass der Übergang für (q,a) undefiniert ist.

4.3.2 Erweiterung von d des NFA

Die Funktion d kann folgendermassen auf eine Funktion d* ausgedehnt werden.

Definition (d*):

(Erweiterung von auf ):

4. Konvention:

4.3.3 Die vom NFA erkannte Sprache

Definition (vom NFA erkannte Sprache):

Sei ein nichtdeterministischer endlicher Automat (NFA). Dann heißt die von M erkannte Sprache.

Anmerkung: Diese Definition impliziert, dass es wenigstens einen Weg von Startzustand aus geben muss, mit dem man über das Wort x in einem Endzustand landet.

4.3.4 Beispiel eines NFA

Wir betrachten den NFA, der die Sprache akzeptiert:

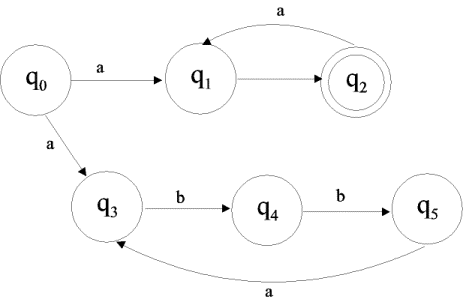
Abbildung 6 – Beispiel eines NFA

Aus diesem Transitionsdiagramm kann man nun die folgenden Transitionen erkennen:

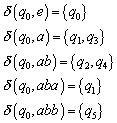
Um diese zu erhalten, geht man wie folgt vor (wir betrachten das Beispiel ):

Betrachte die beiden Zustände . Wohin gelangt man jeweils bei einer weiteren Eingabe von „a“? Von q₂ aus gelangt man nach q₁ (also bilde die Menge {q₁}), von q₄ aus gelangt man mit „a“ nirgendwohin (bilde die leere Menge {}). Dann vereinige die gefundenen Ergebnismengen. Es ergibt sich die Menge {q₁}. Also gilt: .

Wir beweisen nun bei diesem NFA, dass er die Sprache abbildet. Wir verwenden hierbei Induktion.

Induktionsverankerung (n <= 2):

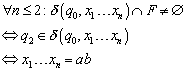
Induktionsschritt:

Man beweise durch Induktion :

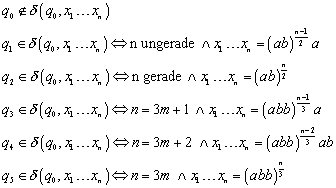
Diese Behauptung müsste nun per Induktion formal bewiesen werden.

Gesamtbeweis

Zusammenfassend mit dem gelungenen Induktionsbeweis folgt also:

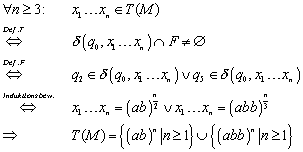
5 Vorlesung vom 20. April 2000

5.1 Über die Äquivalenz von DFA und NFA [1]

Da jeder DFA ein NFA ist, ist es klar[2], dass die Klasse der Sprachen, welche ein NFA akzeptiert die Sprachen enthält, die von einem DFA akzeptiert werden. Es stellt sich jedoch heraus, dass auch nur diese Sprachen von NFA akzeptiert werden. Der Beweis dafür baut darauf auf, dass gezeigt werden kann, dass ein DFA einen NFA simulieren kann. (Für jeden NFA kann ein equivalenter DFA konstruiert werden.) Der DFA simuliert einen NFA indem die einzelnen Zustände des DFA den Mengen von Zuständen des NFA entsprechen. Der so konstruierte DFA überwacht all die Zustände, die der NFA durch die selbe Eingabefolge erreichen (wie der DFA) könnte. Somit gelangt man zu dem folgendem Theorem:

5.1.1 Theorem

Wenn eine akzeptierte Sprache für einen nichdeterministischen endlichen Automaten ist, dann existiert ein deterministischer endlicher Automat, der auch akzeptiert. In anderen Worten: Sei eine Sprache, dann sind folgende Aussagen gleichwertig:

1. für einen deterministischen endlichen Automaten

2. für einen nichtdeterministischen endlichen Automaten

5.1.2 Beweis des Buches

Sei ein NFA, welcher die Sprache akzeptiert. Ein DFA sei dann wie folgt definiert: Die Zustände von sind alle Teilmengen der Menge der Zustände von M. Das heißt: . wird alle Zustände behandeln, welche auch behandeln kann. ist die Menge, der Zustände von , welche einen Endzustand von enthalten. Ein Element von wird dargestellt, als , wobei aus stammen. Zu beachten ist, dass ein einziger Zustand des DFA darstellt. Weiterhin ist .

Wir definieren nun:

dann und nur dann, wenn:

In anderen Worten, angewendet auf von wird berechnet, durch anwenden von auf jeden Zustand von , welcher durch repräsentiert wird. Durch das Anwenden von auf alle und vereinigen der Ergebnisse, erhalten wir eine neue Menge von Zuständen, . Diese neue Menge hat einen Vertreter in und dieser ist der Wert von .

Es lässt sich nun durch Induktion über die Länge eines Eingabestrings zeigen, dass

dann und nur dann gilt, wenn:

Induktionsverankerung:

Man sieht leicht, dass für die Behauptung gilt, da und gleich sein muss.

Induktionsschritt:

Angenommen, die Behauptung ist wahr für Eingaben der Länge . Weiterhin sei eine Kette der Länge mit in . Dann gilt:

Aufgrund der Behauptung ist:

dann und nur dann wahr, wenn:

gilt. Doch mit der Definition von gilt:

dann und nur dann, wenn:

gilt. Somit ist:

dann und nur dann, wenn:

und das unterstützt die Behauptung. Um den Beweis zu vollenden, muss nur noch hinzugefügt werden, dass genau dann zu führt, wenn einen Zustand von enthält, der in liegt. Somit ist

Soweit der Beweis des Buches, in der Vorlesung haben wir den Beweis nur geringfügig anders gehört.

5.1.3 Beweis der Vorlesung

Zur Wiederholung hier noch einmal den zu beweisenden Satz: Sei eine Sprache, dann sind folgende Aussagen gleichwertig:

1. für einen deterministischen endlichen Automaten

2. für einen nichtdeterministischen endlichen Automaten

„Hinrichtung“:

Zuerst zeigen wir hier, mit einfachen Definitionen, aus 1 folgt 2. Gegeben sei ein DFA mit . Dieser Automat akzeptiert die Sprache nach Definition. Nun definieren wir uns dazu einen NFA mit einer Übergangsfunktion .

Diese Übergangsfunktion ist wie folgt definiert:

Aus dieser Definition folgt nun schon, dass ein nichtdeterministischer Automat ist. Der einzige Unterschied zum DFA besteht darin, dass die Übergangsfunktion so definiert ist, dass sie eine Menge von Folgezuständen liefert. In unserem Fall sind dies jedoch alles einelementige Mengen.

Durch Induktion über alle kann man dies zeigen:

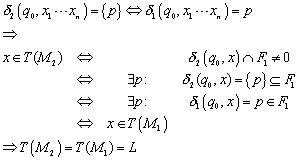
In diesem Beweis ist ausgenutzt worden, dass ein Wort nur dann von einem NFA erkannt wird, wenn die Menge von eine Teilmenge von ist. Dies bedeutet für einen gleichwertigen DFA, dass dieses sein muss, um akzeptiert zu werden. Dies war bei uns nach Definition der Fall.

Rückrichtung:

Nun bleibt noch zu zeigen, dass der umgekehrte Fall gilt. Sprich, wir haben einen NFA gegeben und wollen daraus einen DFA konstruieren. (Aus 2 folgt 1): Hier sei ein NFA mit einer Übergangsfunktion gegeben. Auch dieser Automat soll nach Definition die Sprache akzeptieren.

Wir definieren nun einen DFA wie folgt:

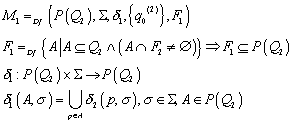
Der so definierte Automat ist ein deterministischer endlicher Automat. Nun bleibt zu zeigen, dass jeder Zustand, den der DFA erreicht, der Menge von Zuständen entspricht, die der NFA erreicht hätte:

Dies wird wieder durch Induktion über die Länge der Eingaben bewiesen.

Induktionsbehauptung:

Induktionsverankerung (n=0):

Man sieht leicht, dass für leere Eingaben der Definition der -Funktion nach das selbe Ergebnis (das Bleiben im Startzustand ) erreicht wird.

Induktionsschritt ():

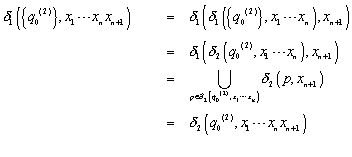
Bei diesem Beweis haben wir folgendes Wissen angewendet. Da es ein DFA ist, nimmt man den Zustand, der mit den ersten Symbolen (Von diesen wissen wir aufgrund der Behauptung, dass für diese die Übergangsfunktion gleichwertig mit ist.) erreicht hat und vereinigt diesen mit dem Zustand, der durch das Symbol erreicht wird. Und die Vereinigung der Teilmengen der ersten Symbole zusammen mit dem Symbolist gleichbedeutend mit der Übergangsfunktion angewendet auf die Symbole . Nun ist noch zu zeigen, dass auch die selben Wörter akzeptiert werden.

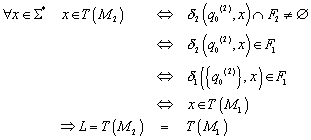
Auch dieser Beweis ist wieder mittels der Definitionen von geführt worden.

Somit steht fest, dass es für alle nichtdeterministischen endlichen Automaten ein deterministischer endlicher Automat existiert für den die folgenden zwei Aussagen gelten:

Die erste Aussage haben wir eben bewiesen. Die zweite Aussage folgt aus der Betrachtung der möglichen Potenzmenge. Hier der kurze Induktionsbeweis.

Induktionsbehauptung:

Für alle mit gilt .

Induktionsverankerung:

Für gilt .

Induktionsschritt ():

Bei der Betrachtung der Symbole steht folgendes fest. Die Anzahl der Teilmengen ohne beträgt . Die Anzahl der Teilmengen mit beträgt . Zusammen gibt dies: . Damit ist die Behauptung gezeigt.

5.1.4 Beispiel 1 (Konstruktion eines DFA aus einem NFA)

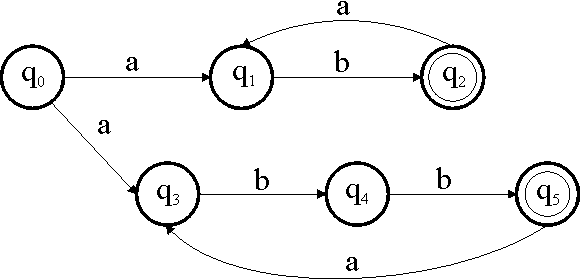
Abbildung 7 – ein nichtdeterministischer, endlicher Automat M

Dieser Automat akzeptiert offensichtlich die Sprache .

Ein deterministischer endlicher Automat könnte so aussehen:

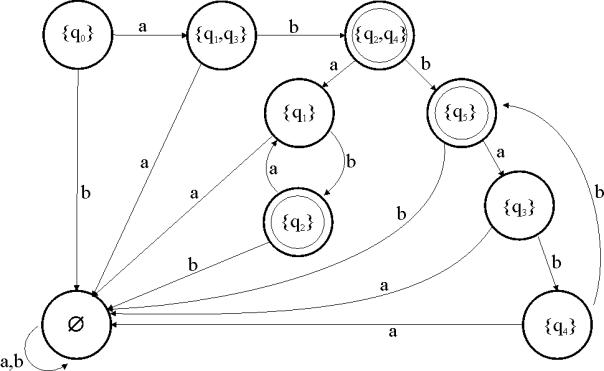
Abbildung 8 - Der DFA, der zu' M äquivalent ist

In diesem Beispiel hat der DFA 9 Zustände, während der NFA 6 Zustände hatte. Und das liegt noch einiges unter den maximal möglichen Zuständen.

5.1.5 Beispiel 2 (Konstruktion eines DFA aus einem NFA)

Hier nun ein etwas komplexeres Beispiel. Es soll ein NFA umgewandelt werden, der die Sprache akzeptiert. Ein solcher NFA kann so aussehen:

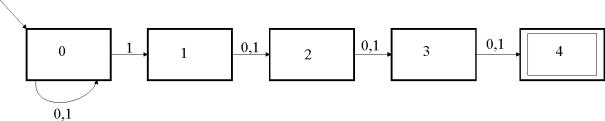
Abbildung 9: NFA zur Sprache L₄

Einen DFA für die Sprache bildet dann:

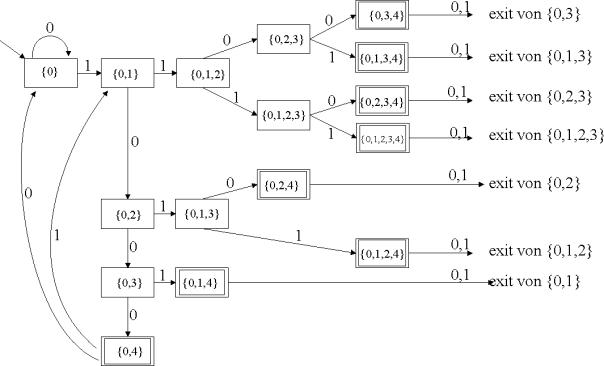
Abbildung 10: der aus dem NFA erzeugte DFA für die Sprache L₄

Bei diesem Beispiel benötigt der NFA 5 Zustände, der DFA jedoch 16 Zustände. Es stellt sich nun die Frage, ob diese Konstruktion auch wirklich minimal ist.

5.2 Satz über die Minimierung von Zuständen

Für alle gilt: Die Sprache kann von einem nichtdeterministischen Automaten mit Zuständen akzeptiert werden. Dann folgt für jeden deterministischen Automaten mit der Sprache .

Beweis:

Sei gegeben. Weiterhin auch ein NFA der diese Sprache akzeptiert, also . Ein Graph dieses Automaten kann wie folgt aussehen:

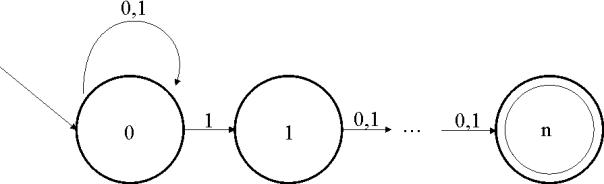
Abbildung 11: NFA für die Sprache Ln

Sei nun weiterhin ein DFA, der die selbe Sprache akzeptiert, also .

Behauptung: Jedes Wort des möglichen Eingabealphabetes (von möglichen Wörtern) muss von dem Automaten unterschieden werden können.

Angenommen zwei gleichlange Wörter aus , die unterschiedlich sind (d.h. sie unterscheiden sich nach einigen gleichen Zeichen an einer Stelle, danach folgt ein Wort z) hätten dieselben Nachfolgezustände.

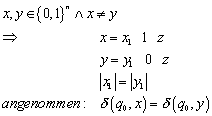
Dann werden entweder beide Wörter akzeptiert, oder aber keines. In beiden Fällen macht der Automat einen Fehler.

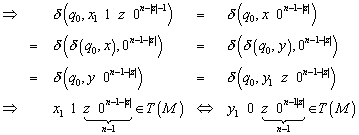
Der Widerspruch liegt darin, dass Element der Sprache ist, jedoch nicht, trotzdem wird für beide Wörter die selbe Entscheidung getroffen, folglich benötigt man für unterschiedliche Eingabewörter unterschiedliche Zustände. Die maximale Anzahl der Zustände beträgt, wie schon vorher gezeigt .

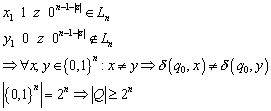
6 Vorlesung vom 25. April 2000

6.1 Nachtrag zur vorherigen Vorlesung

Gegeben ist die folgende (reguläre) Sprache:

Korollar:

Es gibt für jede dieser Sprachen einen nichtdeterministischen, endlichen Automaten, welcher mit n+1 Zuständen auskommt:

Es gibt für jede dieser Sprachen einen deterministischen, endlichen Automaten, welcher mit weniger als 2ⁿ⁺¹ Zuständen auskommt:

Jeder deterministische, endliche Automaten, der eine dieser Sprachen beschreibt, besitzt mindestens 2ⁿ Zustände.

Satz:

Es gibt für jede dieser Sprachen einen nichtdeterministischen, endlichen Automaten, welcher mit n Zuständen auskommt:

Jeder deterministische, endliche Automaten, der eine dieser Sprachen beschreibt, besitzt mindestens 2ⁿ Zustände.

Beweis:

Der Beweis gestaltet sich umfangreich, deswegen wird an dieser Stelle darauf verzichtet.

6.2 Mathematischer Hintergrund

6.2.1 Erweiterung des Begriffes „Äquivalenzrelation“

Unter dem „Index“ einer Äquivalenzrelation versteht man die Maximalzahl paarweise verschiedener Äquivalenzklassen.

6.2.2 Rechts-Invarianz

Eine Äquivalenzrelation auf einer algebraischen Struktur mit einer binären Verknüpfung heißt „rechts-invariant“

6.2.3 Links-Invarianz

Eine Äquivalenzrelation auf einer algebraischen Struktur mit einer binären Verknüpfung heißt „links-invariant“

6.2.4 Kongruenzrelation

Eine Äquivalenzrelation auf einer algebraischen Struktur mit einer binären Verknüpfung heißt „Kongruenzrelation“:

Eine Kongruenzrelation ist eine mit der Struktur verträgliche Äquivalenzrelation. Zum Beispiel ist auf dem Körper der reellen Zahlen die Gleichheitsoperation („=“) bezüglich der Operationen „Addition“ („+“) und „Multiplikation“ („×“) eine Kongruenzrelation:

6.2.5 Quotientenmenge

Eine „Quotientenmenge“ wird auf Basis einer Menge, und einer Kongruenzrelation definiert. Man versteht dann unter der „Quotientenmenge“ die Menge aller Äquivalenzklassen, welche (bezüglich der gegebenen Kongruenzrelation) innerhalb der gegebenen Menge existieren.

Gegeben sei die algebraische Struktur und die Kongruenzrelation „~“. Unter der „Quotientenmenge“ von und ~ versteht man:

6.2.6 Quotientenmonoid

Unter dem „Quotientenmonoid“ versteht man die Zusammenfassung der Quotientenmenge mit einer Operation auf dieser Menge. Die Abbildung (der Elemente der ursprünglichen Menge auf die der Quotientenmenge) definiert man sinnvollerweise als einen Homomorphismus[3]. Die neue Operation für das Quotientenmonoid sei „“.

Das „Quotientenmonoid“ ergibt sich dann als:

Die Rechenregeln für das Quotientenmonoid leiten sich direkt aus der homomorphen Eigenschaft der Abbildung her:

Man sieht an der obigen Herleitung, wie bedeutsam die Eigenschaften „Kongruenz“ und „Transitivität“ der Kongruenzrelation „~“ für die Quotientenmenge sind.

Beispiel 1:

Gegeben sei die Menge der natürlichen Zahlen mit der Verknüpfung „×“ (Multiplikation), und ein Modul m. Zwei Zahlen gelten als äquivalent bezüglich „~“, wenn sie den gleichen Rest bei einer Division durch m abwerfen:

Gemäß dieser Definition ist z.B. bei m=5 die Zahl 11 äquivalent zu 31: 11~31. Es handelt sich bei „~“ um eine Äquivalenzrelation, da die Bedingungen Reflexitivität, Transitivität und Symmetrie erfüllt sind (der Nachweis dieser Eigenschaften sollte keine Probleme bereiten).

Es handelt sich bei „~“ aber nicht nur um eine Äquivalenzrelation, sondern sogar um eine Kongruenzrelation. Der Nachweis hierfür ist etwas aufwendiger:

Nach gilt:

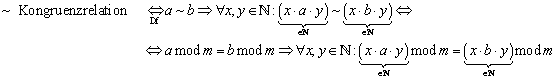
Die abschließende Implikation sollte nach kurzem Nachdenken für jedermann ersichtlicherweise korrekt sein; ein Beweis an dieser Stelle ist nicht nötig.

Daher gelten gemäß und die folgenden Rechengesetze:

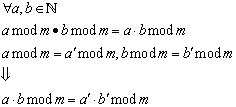
6.3 Reguläre Ausdrücke

6.3.1 Kleenesche Hülle

Sei S eine endliche Menge von Symbolen und seien L, L₁ und L₂ Mengen von Zeichenketten aus S*. Die Konkatenation von L₁ und L₂ – geschrieben als L₁L₂ – ist die Menge . Die Zeichenketten in L₁L₂ werden gebildet, indem man an eine aus L₁ gewählte Zeichenkette eine Zeichenkette aus L₂ anhängt und das in allen möglichen Kombinationen. Wir definieren nun:

L* bezeichnet also alle Wörter, die durch die Konkatenation einer beliebigen Anzahl von Wörtern aus L entstehen.

Beispiel:

Sei und . Dann ist . Ebenso gilt .

6.3.2 Reguläre Ausdrücke

Die von endlichen Automaten akzeptierten Sprachen lassen sich durch einfache Ausdrücke beschreiben, die als „reguläre Ausdrücke“ bezeichnet werden. Auf Grund dieser Äquivalenz werden die Sprachen der endlichen Automaten auch „reguläre Mengen“ genannt.

Oder umgekehrt: Reguläre Ausdrücke bilden einen Formalismus zur Beschreibung formaler Sprachen.

Zwei reguläre Ausdrücke heißen „äquivalent“, wenn sie die gleiche formale Sprache beschreiben (z.B. [ab]*a und a[ba]*). Die Äquivalenz regulärer Ausdrücke lässt sich über algebraische Gesetze zeigen.

6.3.3 Reguläre Ausdrücke vs. endliche Automaten

Satz:

Die folgenden drei Aussagen sind äquivalent:

3. L ist reguläre Sprache/reguläre Menge

4. L ist die Vereinigung von einigen Äquivalenzklassen einer rechts-invarianten Äquivalenzrelation von endlichem Index.

5. Sei R_L eine Relation, die wie folgt definiert ist:

Dann ist R_L von endlichem Index.

Beweis:

1 Þ 2:

Wenn L eine reguläre Menge ist, dann existiert ein endlicher Automat (DFA/NFA), der exakt diese Menge beschreibt:

Sei r eine Äquivalenzrelation, welche alle Wörter aus S*, die zu dem selben Zustand des Automaten führen, in einer Äquivalenzklasse zusammenfasst:

Die Äquivalenzrelation r ist rechts-invariant:

Dann lässt sich hieraus die Behauptung folgern:

Wieso lässt sich diese Behauptung folgern? Nun, gehen wir von dem Gegenteil aus, nämlich dass . Das würde bedeuten, dass es mehr Wörter gibt, als es Zustände gibt, die aber dennoch alle zu verschiedenen Zuständen führen. Der Widerspruch dieser Annahme liegt auf der Hand.

Damit lässt sich die reguläre Menge L darstellen als Menge der Eingabewörter, welche zu einem der akzeptierenden Zustände des Automaten führt. Jeder akzeptierende Zustand des Automaten kann bezüglich der Äquivalenzrelation (definitionsgemäß) nur von einer Klasse von Eingabewörtern erreicht werden.

Die reguläre Menge L können wir darstellen als Vereinigung aller akzeptierenden Zustände des Automaten, und damit als Vereinigung einiger Äquivalenzklassen einer rechts-invarianten Äquivalenzrelation von endlichem Index:

2 Þ 3:

Im vorangegangenen Teil wurde die Äquivalenzrelation r eingeführt, diese benutzen wir weiterhin. Darüber hinaus definieren eine (zweite) Äquivalenzrelation R_L wie folgt:

Die Definition der Äquivalenzrelation R_L ist etwas kompliziert. Textuell formuliert bedeutet , dass alle jenen Wörter aus S* in Relation stehen, die a) entweder beide in der Sprache enthalten sind, oder beide nicht in der Sprache enthalten sind; und b) die Bedingung a) auch dann noch erfüllen, wenn ihnen ein beliebiges Wort „angehängt wird“.

Die Definition dieser Äquivalenzrelation erinnert an die Zustandsminimierung via Implikationstafel. Man bezeichnet dabei alle Zustände als „äquivalent“, die bei den selben Eingabesymbolen in die selben Nachfolgezustände, oder in äquivalente Nachfolgezustände überführt werden.

Behauptung:

Beweis zu :

Bei dem Beweis machen wir uns die Tatsache zunutze, dass die Äquivalenzrelation r rechts-invariant ist:

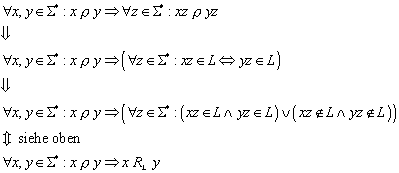
Aus der Tatsache, dass jedes Paar von Eingabewörtern aus S*, dass in der Äquivalenzrelation r enthalten ist, automatisch auch in der Äquivalenzrelation R_L enthalten ist, resultiert, dass die Äquivalenzklasse eines beliebigen Eingabewortes bezüglich der Äquivalenzrelation r eine Teilmenge der Äquivalenzklasse bezüglich der Äquivalenzrelation R_L ist:

Daraus folgt, dass es bezüglich der Äquivalenzrelation r mindestens so viele (disjunkte) Äquivalenzklassen geben muss, wie bezüglich der Äquivalenzrelation R_L:

Daraus wiederum folgt, dass auch der Index der Äquivalenzrelation R_L endlich sein muß:

2 Þ 3:

Behauptung:

Die Äquivalenzrelation R_L ist rechts-invariant.

Beweis:

6.4 Nerode Automat

6.4.1 Definition des Nerode Automaten

Mit dem bisher erlangten Wissen, ist es möglich, einen minimalen Automaten zu erstellen, der eine reguläre Sprache repräsentiert. Dieser Automat heißt „Nerode Automat“.

Zur Konstruktion des Nerode Automaten wird erneut die Äquivalenzrelation R_L herangezogen, die wie folgt definiert ist:

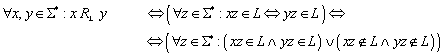
Die Menge der unterschiedlichen Äquivalenzklassen, die durch R_L definiert werden, wird im Folgenden mit „Q_N“ bezeichnet:

Der Nerode Automat ist definiert als:

mit

d_N ist damit wohldefiniert.

6.4.2 Repräsentantenunabhängigkeit des Nerode Automaten:

Im Folgenden wird gezeigt, dass die Übergangsfunktion d_N wohldefiniert ist, d.h. ihre Definition repräsentantenunabhängig ist. Dazu ist es nötig, zu zeigen, dass die Übergangsfunktion für alle Eingabewörter, die äquivalent sind, den selben Nachfolgezustand liefert.

Zu zeigen:

Beweis:

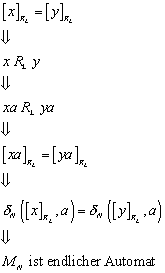
6.4.3 Regularität des Nerode Automaten:

Im Folgenden wird bewiesen, dass die Sprache, die der Nerode Automat erzeugt/definiert, eine reguläre Sprache ist.

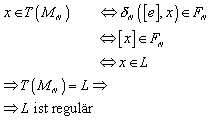
6.4.4 Minimalität des Nerode Automaten

Im Folgenden wird bewiesen, dass der Nerode Automat minimal ist, d.h. dass jeder endliche Automat, der die selbe Sprache L definiert, mindestens genauso viele Zustände haben muß wie M_N.

Satz:

Der Nerode Automat ist minimal.

Beweis:

Der Beweis ist ein Widerspruchsbeweis. Es wird angenommen, dass sehr wohl ein Automat existiert, der die selbe Sprache L definiert, der aber mit weniger Zuständen auskommt:

Die Definition der Äquivalenzrelation r wird aus , und übernommen:

Weil die Menge Q_N der Menge der Äquivalenzklassen entspricht, die durch die Äquivalenzrelation R_L definiert werden (siehe ), gilt:

Aus , , und folgt:

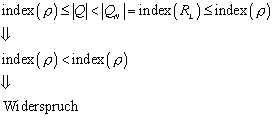
6.4.5 Eindeutigkeit des Nerode Automaten

Satz:

Sei ein minimaler Automat für eine Sprache L mit . Sei der Nerode Automat für L mit . Dann ist M isomorph zu M_N. D.h. es existiert ein Isomorphismus

Beweis:

Weil sowohl M als auch M_N minimal sind, müssen sie über die gleiche Anzahl an Zuständen verfügen:

Sei h() so definiert, dass es jeden Zustand q aus der Menge der Zustände Q auf eine Äquivalenzklasse bezüglich der Äquivalenzrelation R_L abbilde (wir erinnern uns: die Äquivalenzklassen bezüglich der Äquivalenzrelation R_L liegen dem konstruierten Nerode Automaten zugrunde).:

7 Vorlesung vom 27. April 2000

7.1 Nerode Automat

7.1.1 Homomorphismus und Isomorphismus

Gegeben seien zwei Gruppen S₁ und S₂ mit und . Eine Abbildung heißt Homomorphismus, wenn für alle gilt

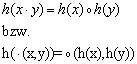
Eine Illustration verdeutlicht das

Abbildung 12 - Homomorphismus

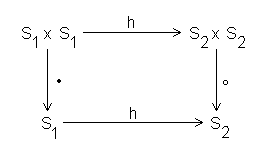
Ist eine homomorphe Abbildung bijektiv, so wird sie isomorph genannt. Man sagt, die Struktur beider Gruppen ist gleich, sie unterscheiden sich nur in den Bezeichnungen der Elemente.

7.1.2 Minimalität und Eindeutigkeit des Nerode Automaten

Nachdem in den vorangegangenen Abschnitten gezeigt wurde, dass der Nerode Automat minimal ist, vergleichen wir ihn jetzt mit anderen minimalen Automaten. Dabei werden wir feststellen, dass alle minimalen Automaten (DFA) einer Sprache L die gleiche "Verdrahtung" ihrer Zustände haben und sich lediglich in der Bezeichnung der Zustände unterscheiden, sie also isomorph sind.

Sei L eine Sprache, die von einem minimalen Automaten M und dem Nerode Automaten M_N erkannt wird

dann seien M und M_N wie oben beschrieben isomorph, d. h. es existiert ein Homomorphismus

Das wird in folgendem Schaubild illustriert

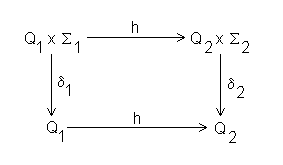
Abbildung 13 - Homomorphismus zwischen Automat M und Nerode Automat

Es existiert eine Abbildung h, die alle Zustände von M in Zustände in M_N (Äquivalenzklassen) überführt. Formal ausgedrückt

Hier stellt sich die Frage, ob h eindeutig definiert ist. Alle Wörter x und y, die den Automaten M in den gleichen Zustand überführen, müssen auch M_N in die gleiche Äquivalenzklasse überführen. Zu Zeigen ist, dass x und y der gleichen Äquivalenzklasse von R_L angehören.

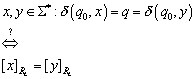
Beweis:

Zum Beweis führen wir eine neue Äquivalenzrelation ~ ein

Überführen zwei Wörter x und y den Automaten in den gleichen Zustand, so sind sie äquivalent. Da die Anzahl der Zustände der oben betrachteten Automaten minimal und gleich ist, gilt für den Index (die Anzahl der maximal paarweise verschiedenen Äquivalenzklassen) der ~ Relation

Weiterhin gelte

Somit ist h als eindeutige Abbildung von Zuständen Q auf Äquivalenzklassen aus Q_N definiert.

Könnte es Zustände q in Automat M geben, für die h(q) nicht definiert ist?

Wenn ein solcher Zustand existieren würde, dann gebe es kein Wort x, dass den Automaten in diesen Zustand überführt und der Zustand somit überflüssig. Damit wäre M nicht mehr minimal und ein Widerspruch läge vor. h ist für alle Zustände q aus Q definiert.

Surjektivität von h

Injektivität von h

Wenn zwei verschiedene Zustände aus Q sind und [x] und [y] ihre Abbildungen in Q_N, dann gilt

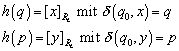
Dann sind x und y nicht äquivalent zueinander (bezüglich der ~ Relation) und damit gilt Injektivität von h ( gilt immer).

Isomorphismus von h

Da h injektiv und surjektiv, ist die Abbildung bijektiv. h ist daher ein Isomorphismus. Für einen Zustand q existiert ein x, dass den Automaten M in diesen Zustand überführt.

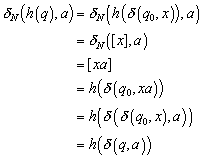
Die Herleitung zeigt, dass es egal ist, ob die Konkatenation von x und a zunächst in der Urmenge (die Zustände von Q) stattfindet und dann nach Q_N abgebildet wird oder umgekehrt.

Damit ist h isomorph und als Korollar kann festgestellt werden, dass alle minimalen Automaten (DFA) isomorph sind. Anders ausgedrückt sind alle minimalen Automaten bis auf Isomorphien eindeutig bestimmt. Die Verdrahtung der Zustände ist gleich, lediglich die Zustandsbezeichnung kann variieren.

7.2 Minimierung von endlichen Automaten

7.2.1 Rekursion der k Relationen

Endliche Automaten können sich in einem nicht minimalen Zustanden befinden. Mit einiger Logik und Transformation lassen sie sich in minimale Automaten überführen, die isomorph zum Nerode Automaten sind (wenn es sich denn um DFAs handelt - bei NFAs ist die Anzahl der nicht isomorphen minimalen Automaten u. U. beliebig groß).

Für die Minimierung - auch Zustandsreduktion genannt - führen wir zunächst eine neue Äquivalenzrelation k zwischen zwei Zuständen q und q' ein. Zustände sind bezüglich k äquivalent, wenn sie Wörter x, deren Länge kleiner gleich k ist, in einen Endzustand überführen oder beide Zustände die Wörter nicht in einen Endzustand überführen.

Der Betrachtung zugrunde liegt ein endlicher Automat mit q und q' Zuständen aus Q. Dann seien folgende Äquivalenzrelationen definiert

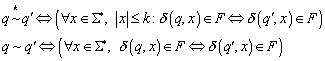
Scheinbar besteht zwischen der auf eine Wortlänge k beschränkten und der allgemeinen ~ Relation ein Zusammenhang. Daher behaupten wir

Behauptung:

Beweis:

Die genau-dann-wenn Beziehung der obigen Behauptung beweisen wir in beide Richtungen. Wenn die k Relation gilt, dann muß auch die k-1 Relation gelten, da die k Relation alle Wörter enthält, die auch in k-1 enthalten sind.

Seien ein Wort und ein Zeichen beliebig gewählt, dann gilt

und die Zustände q und q' gehören zur k-1 Relation

Damit ist gezeigt

Gilt bereits die k-1 Relation, so zeigen wir, dass die Behauptung in der anderen Richtung gilt. Für gilt

Sei und . Dann läßt sich zeigen

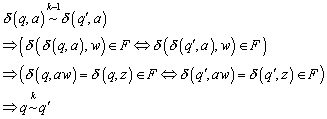
Somit gilt die Behauptung auch in der anderen Richtung

7.2.2 Verfeinerung von Äquivalenzrelationen

Zwischen Äquivalenzrelationen lassen sich Beziehungen ausdrücken, d. h. sie können kongruent oder verschieden sein. Nehmen wir die beiden Äquivalenzrelationen r₁ und r₂ die auf der Menge S liegen. Sind die r₁ und r₂kongruent, dann

Andernfalls ist eine Relation kleiner oder echt kleiner als die andere. Man spricht von Verfeinerung

7.2.3 Anwendung auf k Relation zur Zustandsreduktion

Betrachtet man die k Relationen, dann enthält die k Relation höchstens gleich viele Zustände wie die k‑1 Relation. k ist daher eine Verfeinerung von k-1

Wir behaupten zudem

Beweis:

Die Behauptung kann man durch Induktion beweisen. Für s = 0 ist die Aussage klar, da es sich um dieselbe Relation k handelt. Für alle weiteren nehmen wir an, dass

bereits gelte. Dann kann man auf k+s+1 gehen

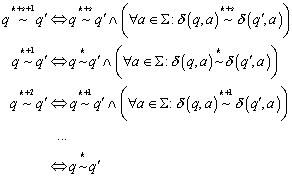
Korollar:

Der Index der k‑1 Relation ist kleiner als der der k Relation

Damit haben wir als Ausgangspunkt für weitere Betrachtungen folgende Aussagen zusammengestellt

8 Vorlesung vom 2. Mai 2000

8.1 Minimierung mittels Nerode Automaten

8.1.1 Satz über die Gleichwertigkeit von Relationen

Sei ein endlicher deterministischer Automat mit der Mächtigkeit . Dann gilt: .

Der Beweis der „Hinrichtung“. ist trivial und folgt auch schon aus dem Satz der letzten Vorlesung. Die „Rückrichtung“ ist da schon komplizierter. Der Beweis erfolgt indirekt. Angenommen die beiden Relationen währen nicht identisch:

Grundsätzlich gilt, dass ~ eine Verfeinerung von ist. Damit muss eine echte Verfeinerung von sein, denn sonst wäre ja , was ein Widerspruch zur Annahme wäre.

Durch eine Betrachtung der Anzahl der Klassen der Zustände () erkennt man schnell, dass es mindestens eine Klasse von Zuständen geben muss, und zwar die der akzeptierenden Zustände. Da weiterhin gilt, dass eine echte Verfeinerung von ist, sind alle anderen Relationen echte Verfeinerungen (also gilt ). Die Anzahl der Klassen wächst durch jeden Index um eins. Führt man diesen Gedankengang fort und beachtet, dass es alles echte Verfeinerungen sind, so gelangt man für den zu dem Schluss, dass dieser mindestens Klassen enthalten muss.

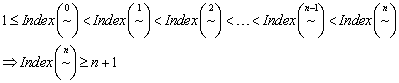
Dies ist allerdings ein Widerspruch, da es höchstens (mit ) Äquivalenzklassen auftreten können.

8.1.2 Konstruktion eines minimalen Automaten

Sei nun ~ weiterhin wie bisher definiert. Dann gibt es zu dem endlichen Automaten einen äquivalenten minimalen Automaten . Dabei ist:

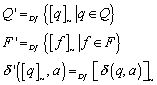
Dieser Automat wird wie folgt konstruiert, als Zustände nehme man die Äquivalenzklassen der Zustände. Als akzeptierte Zustände gelten die Äquivalenzklassen der Tilderelation von F.

Damit ist ein minimaler Automat mit .

Aber ist dieser Automat auch wirklich minimal, oder nur ein reduzierter Automat? Gezeigt wird dies durch den folgenden Beweis:

ist mit :

wohldefiniert, aus folgendem Grund: Wenn und in der selben Äquivalenzklasse liegen und die Relation definiert sind, dann ist auch mit in Relation.

Mit der Definition von gilt dann:

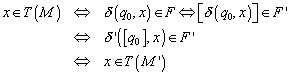
Somit akzeptieren also beide Automaten die selbe Sprache. Die Frage ist nun, ob dieser Automat auch minimal ist.

Zuerst definieren wir die Relation als:

Weiterhin wissen wir über diesen Automaten, dass der , da jeder Zustand erreichbar ist. Somit wissen wir, dass die Relation die Nerode-Automat Relation verfeinert:

Gilt nun auch, die Umkehrung? Folgt aus ? Der Beweis erfolgt durch Kontraposition.

Die Klassen können nicht gleich sein, da es die Elemente nicht in der ~ Relation gibt. Es gibt daher ein Element z, so dass:

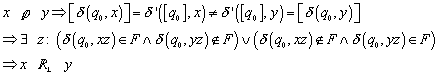
Die beiden Relationen sind also gleichwertig: . Und die Minimalzahl der Zustände ist: Und damit ist gezeigt, dass der Automat minimal ist.

8.2 „Praktische“ Minimierung von deterministischen endlichen Automaten

Nachdem wir wissen, dass die Bestimmung der Äquivalenzklassen definiert ist für:. Eine Konstruktion, die den (bis auf Isomorphie) eindeutig bestimmten minimalen endlichen Automaten ( mit ) liefert benötigt die folgende Eigenschaft:

8.2.1 Der „Algorithmus“

Sei ein endlicher Automat. Dann gelangt man durch die folgenden Schritte zu dem minimalen Automaten:

1. Man beseitige alle nicht-erreichbaren Zustände, d.h. alle Zustände q, für die gilt . (Es stellt sich natürlich die Frage, in wie weit dieses Problem algorithmisch lösbar ist. Ein möglicher Algorithmus könnte alle durch Wörter der Länge erreichbaren Zustände betrachten. Damit kommt man durch alle erreichbaren Zustände.)

2. hat maximal zwei Äquivalenzklassen. Zum einen die akzeptierenden Zustände und dann noch die nicht akzeptierenden Zustände:

3. Angenommen, man hat die Äquivalenzklassen der Relation für , dann bestimmt man die Klassen der Relation wie folgt:

Zunächst wird nun die folgende Tabelle aufgestellt:

Alle Felder erhalten also als Eintrag . Nun formt man die Klassen von , indem man alle Zustände, die bereits bei in einer Klasse waren und die in obiger Liste gleiche „Zeilen“ haben in jeweils eine Klasse der Relation schreibt.

4. Wenn nun äquivalent zu ist (was, wie schon gezeigt, spätestens bei eintreten muss), dann bricht das Verfahren ab. Wir bilden dann die ~ Relation durch Setzen, von .

5. Der minimale Automat wird letztlich wie oben schon beschrieben konstruiert:

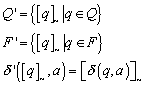
8.2.2 Beispiel

Wir betrachten einen Automaten , welcher die Sprache akzeptieren soll. Ein Automat, der dies löst ist in folgender Grafik aufgelistet. Dabei ist zu beachten, dass der Zustand 7 nicht erreicht werden kann.

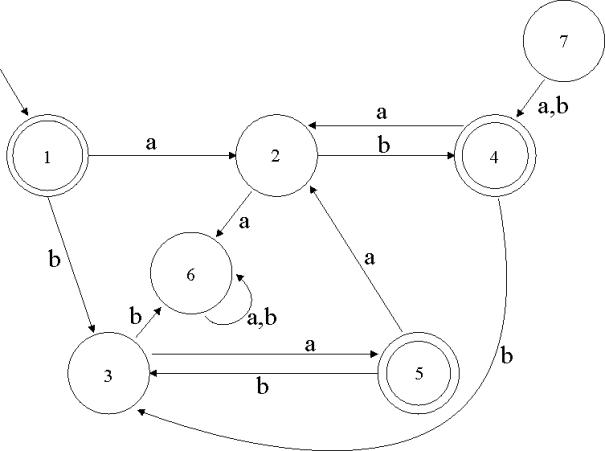
Abbildung 14: Beispiel eines nicht minimalen Automaten

Durch das Anwenden des oben beschriebenen Algorithmus gelangt man schnell zu folgender Tabelle:

:		Fehler! Es ist nicht möglich, durch die Bearbeitung von Feldfunktionen Objekte zu erstellen.

:	a	b
	1. 2. 3. 4. 5. 6.
	Folglich sind die Klassen von :
:	a	b
	1. 2. 3. 4. 5. 6.
	Folglich sind die Klassen von :

An dieser Stelle sind wir dann auch schon fertig, da wir sehen, dass die Klassen und schon äquivalent sind, somit ist die ~ Relation definiert durch:

Es bleibt nur noch den endgültigen Automaten aufzustellen. Dieser sieht dann, so aus, wie in der folgenden Abbildung gezeigt.

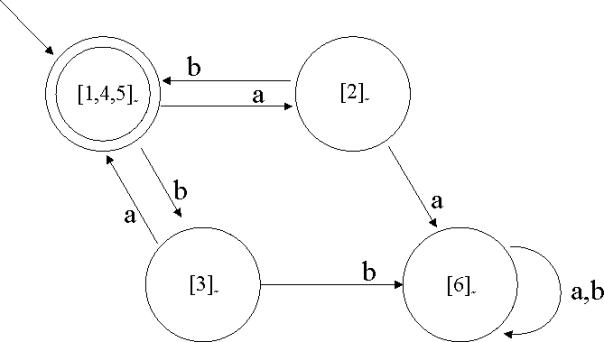
Abbildung 15 der minimierte Automat M'

9 Vorlesung vom 04. Mai 2000
Abschlußeigenschaften regulärer Mengen

9.1 Motivation

Viele Operationen auf regulären Mengen erhalten die Eigenschaft der Regularität. Dies bedeutet, daß die Operationen angewandt auf den regulären Mengen wieder zu einer regulären Menge führt.

Mit Hilfe dieser als Abgeschlossenheit bezeichneten Eigenschaften kann man also aus gegebenen regulären Mengen wieder neue Mengen schaffen, die von endlichen Automaten akzeptiert werden.

Man kann die Abschlußeigenschaften auch dazu verwenden, um zu zeigen, dass eine bestimmte gegebene Sprache regulär (bzw. nicht regulär) ist, indem man über die Abschlußeigenschaften auf bereits bekannte Sprachen zurückgeht.

9.2 Sammlung von Abschlußeigenschaften

Es gelten die folgenden Abschlußeigenschaften regulärer Mengen:

Vereinigung:

Konkatenation:

Kleenesche Hülle:

Komplement:

Schnitt:

Homomorphishmus:

inv. Homomorphism.:

9.2.1 Beweise Vereinigung, Konkatenation, Kleenesche Hülle

Zu , und findet man die entsprechenden Beweise im Beweis über die Äquivalenz von regulären Ausdrücken und einem NFA mit e-Bewegungen.

9.2.2 Komplementbildung

Zu Zeigen:

Beweis:

Sei ein DFA mit L=T(M). Dann definieren wir einen DFA M‘ wie folgt:

Es zeigt sich nun folgendes:

Fehler! Es ist nicht möglich, durch die Bearbeitung von Feldfunktionen Objekte zu erstellen.

Also:

9.2.3 Schnitt

Zu zeigen:

Beweis:

Dies zeigt man sehr schnell über die Regeln von deMorgan. Es gilt nämlich und mit der Abgeschlossenheit unter Komplement- und Vereinigungsbildung folgt automatisch die Abgeschlossenheit unter Schnittbildung.

9.2.4 Substitution

Definition:

Eine Substitution f ist eine Abbildung . F assoziiert also mit jedem Symbol aus S eine Sprache. Wir erweitern f auf Zeichenketten:

Beispiel:

Ist . Damit ist f(010) die reguläre Menge .

Satz:

Die Klasse der regulären Mengen ist unter Substitution abgeschlossen.

Beweis:

Sei eine reguläre Menge und . Sei weiter die Substitution, die durch f(a)=R_a definiert ist.

Wir wählen reguläre Ausdrücke zur Bezeichnung von R und allen R_a.

Man ersetze nun jedes Auftreten des Symbols a im regulären Ausdruck für R durch den regulären Ausdruck für R_a.

Um zu beweisen, dass der resultierende reguläre Ausdruck beschreibt, wird verwendet, dass die Substitution einer Vereinigung, eines Produkts oder einer Hülle gleich der Vereinigung, dem Produkt bzw. der Hülle der Substitution ist (also homomorph).

Mit einer Induktion über die Anzahl der Operatoren im regulären Ausdruck vervollständigt man leicht den Beweis.

9.2.5 Homomorphismus

Zu zeigen:

Beweis:

Die Abgeschlossenheit unter Homomorphismen folgt sofort aus der Abgeschlossenheit unter Substitutionen, da ein Homomorphismus ein Spezialfall der Substitution ist, bei der h(a) für alle a gegeben wird.

9.2.6 Inverser Homomorphismus

Zu zeigen:

Beweis:

Es seien und ein Homomorphismus.

Wir konstruieren einen DFA M₁, der akzeptiert, indem er ein Symbol a aus S₁ liest und M₁ auf h(a) simuliert. Wir geben die Definition an:

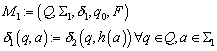
Zu beachten ist, dass h(a) eine lange Zeichenkette oder aber auch das leere Wort sein kann. Dies ist aber kein Problem, da d mittels Erweiterung auch auch Zeichenketten operiert.

Durch Induktion über die Wortlänge des Wortes x kann man leicht zeigen, dass gilt

Daher wird x von M₁ genau dann akzeptiert, wenn h(x) von M₁ akzeptiert wird. Wir haben also einen DFA gebaut mit . Damit gilt auch .

10 Vorlesung vom 9. Mai 2000

10.1 Beispiele zur Nutzung der Abschlusseigenschaften

10.1.1 Einleitung

Aus den vorhergehenden Vorlesungseinheiten sind die sogenannten „Abschlusseigenschaften“ bekannt:

Weiterhin nehmen wir zur Kenntnis[4]:

In den folgenden Beispielen wird durch die Kombination des Wissens von mit den Aussagen der Abschlusseigenschaften der Beweis für einen neuen Zusammenhang erbracht.

Behauptung:

Die folgende Aussage ist falsch: „Wenn aⁿbⁿ nicht regulär ist, kann auch eine „größere“ Sprache wie a^*b^* nicht regulär sein.“ Tatsächlich gilt, dass aⁿbⁿ nicht regulär ist, und a^*b^* regulär ist.

10.1.2 Beispiel 1

Zu zeigen sei:

Wir führen einen Widerspruchsbeweis durch, und nehmen an:

Wir definieren eine homomorphe Funktion h() wie folgt:

lässt sich mit Hilfe von umschreiben zu:

Gemäß gilt:

Aus und folgt:

10.1.3 Beispiel 2

Zu zeigen sei:

Wir führen einen Widerspruchsbeweis durch, und nehmen an:

Wir definieren eine zweite Sprache L₁ wie folgt:

Aus folgt, dass die Schnittmenge zweier regulärer Mengen erneut regulär ist, daher folgt:

lässt sich umschreiben zu:

Aus und folgt:

10.1.4 Beispiel 3

Zu zeigen sei:

Wir führen einen Widerspruchsbeweis durch, und nehmen an:

Wir definieren eine homomorphe Funktion h() wie folgt:

lässt sich mit Hilfe von umschreiben zu:

Gemäß gilt:

Aus und folgt:

10.1.5 Beispiel 4

Zu zeigen sei:

Wir führen einen Widerspruchsbeweis durch, und nehmen an:

Wir definieren eine zweite Sprache L₁ wie folgt:

Aus folgt, dass das Komplement einer regulären Menge, und auch die Schnittmenge zweier regulärer Mengen erneut regulär ist, daher folgt:

Wir definieren eine homomorphe Funktion h() in eine weitere, neue Sprache L₂ wie folgt:

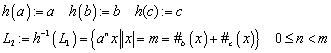
Aus folgt, dass die umgekehrte Anwendung einer homomorphen Abbildung auf eine reguläre Menge erneut regulär ist:

Wir definieren nun eine dritte Sprache:

Aus folgt, dass die Schnittmenge zweier regulärer Menge erneut regulär ist:

Wir definieren eine zweite, homomorphe Funktion h() in eine weitere, neue Sprache L₄ wie folgt:

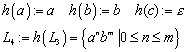
Wir definieren nun eine fünfte Sprache:

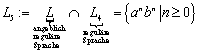
Aus folgt, dass die Schnittmenge zweier regulärer Menge erneut regulär ist:

10.1.6 Beispiel 5

Wir verwenden dieses Mal ein erweitertes Alphabet S:

Zu zeigen sei:

Wir führen einen Widerspruchsbeweis durch, und nehmen an:

Wir definieren eine homomorphe Funktion h() wie folgt:

Gemäß gilt:

Aus und folgt:

Der Widerspruch entsteht durch die Aussage von .

10.2 Automaten mit e-Bewegungen

10.2.1 Einleitung

Bisher sind der deterministische endliche Automat (DFA) und der nichtdeterministische endliche Automat (NFA) betrachtet worden, wobei der DFA lediglich ein Spezialfall des NFA war. Diese Automaten haben sich dadurch ausgezeichnet, dass jede Transition (jeder Zustandswechsel) durch ein Eingabesymbol ausgelöst wurde.

Bei den im Folgenden betrachteten „Automaten mit e-Bewegungen“ gibt es Transitionen, die durch das Eingabesymbol „e“, d.h. das „leere Wort“ ausgelöst werden.

Das Transitionsdiagramm eines derartigen Automaten kann z.B. wie folgt aussehen:

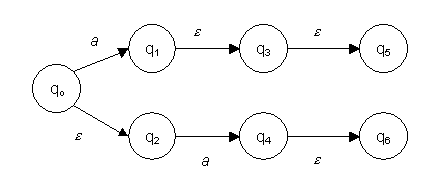
Abbildung 16 – ein Transitionsdiagramm

Bei dem obigen Automaten führt aus dem Startzustand q₀ für das Eingabezeichen a lediglich ein direkter Pfad zu dem Zustand q₁. Allerdings führen zahlreiche weitere Pfade für das Eingabesymbol e zu den restlichen Zuständen.

Das Eingabesymbol e unterscheidet sich von allen anderen Eingabesymbolen, und zwar insofern, als dass es der Automat „jederzeit“ einlesen kann – unabhängig von den wirklichen Eingabesymbolen.

Der obige Automat kann also für das Eingabezeichen a in jeden, eingezeichneten Zustand wechseln. Um dieses Verhalten beschreibungstechnisch in den Griff zu kriegen, definiert man den Begriff der e-Hülle (siehe folgender Abschnitt).

10.2.2 e-Hülle

Man bezeichnet die Menge aller Konten p, zu denen es einen mit e bezeichneten Weg vom Knoten q gibt, als e-Hülle(q)[5].

Für den Automaten aus Abbildung 16 gilt, dass alle Knoten vom Startzustand aus erreichbar sind, also:

Definitionsgemäß ist jeder Knoten/Zustand in seiner eigenen e-Hülle enthalten. Man kann sich das so vorstellen, als dass von jedem Knoten ein mit e markierter Übergang auf sich selber existiert, den man beim Zeichnen weglässt:

Auf das obige Beispiel angewendet ergibt sich die e-Hülle wie folgt:

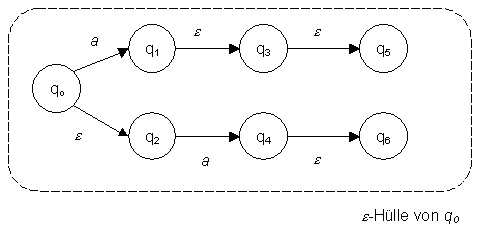
Abbildung 17 – die Epsilon-Hülle im Transitionsdiagramm

10.2.3 Formale Unterschiede zum gewöhnlichen NFA

Die Definition des Automaten mit e-Bewegungen entspricht der des „normalen“ NFA:

Der einzige Unterschied zum „normalen“ NFA ist die Übergangsfunktion d, die nun wie folgt definiert ist:

Die Erweiterung der Übergangsfunktion d (die nur für einzelne Symbole taugt) auf ganze Eingabewörter geschieht mit Hilfe der Übergangsfunktion . soll als Ergebnis die Menge aller Zustände liefern, zu denen es von q aus einen mit w markierten Pfad gibt, welcher e-Kanten beinhalten darf:

Anmerkung: Beim Automaten mit e-Bewegungen können die Ergebnisse von und verschieden sein; zwischen und muss also unterschieden werden.

10.2.4 Äquivalenz vom NFA mit und ohne e-Bewegungen

Auch die e-Bewegungen erlauben es dem Automaten nicht, mehr als reguläre Mengen zu akzeptieren. Der Automaten mit e-Bewegungen reiht sich damit in die Klasse von NFA und DFA ein.

Wir werden uns darauf beschränken, zu zeigen, dass jeder NFA mit e-Bewegungen durch einen „normalen NFA“ ersetzt werden kann. Der Beweis in der umgekehrten Richtung ist zwar theoretisch ebenfalls nötig, erübrigt sich aber bei näherer Betrachtung[6].

Zu einem gegebenen e-NFA definieren wir einen „normalen“ NFA . Wie man an der Definition sehen kann, muss an dem Automaten nicht viel verändert werden. Die Menge der akzeptierenden Zustände F kann weitestgehend übernommen werden, abgesehen von der Ausnahme, dass die e-Hülle von q₀ einen akzeptierenden Zustand enthält:

Diese Veränderung ist nötig, weil M’ keine e-Transitionen kennt. Tritt nämlich der Fall ein, dass die e-Hülle von q₀ einen akzeptierenden Zustand enthält, dann würde M ja beenden, ohne ein einziges Zeichen gelesen zu haben. Für M’ lässt sich dies nur nachbilden, indem der Startzustand (q₀) selber akzeptierend ist. Und genau das erreichen wir mit der obigen Fallunterscheidung.

Nun wird noch eine Übergangsfunktion benötigt. Dazu behalten wir die bereits definierte Funktion bei:

Wie kann das sein? Fangen wir ganz vorne an. Wir möchten zwei äquivalente Automaten erhalten. Wir haben bereits definiert, dass beide Automaten auf der selben Menge von Zuständen operieren. Was ist nun also naheliegender, als auch die Übergangsfunktion komplett zu übernehmen? Genau dies tun wir laut . Der Sicherheit halber werden wir aber im folgenden beweisen, dass es auch richtig ist, was wir da tun... Wir betrachten zunächst einmal den einfachsten Fall, nämlich, dass die Eingabe ein einzelnes Symbol ist: Dann folgt aus , und :

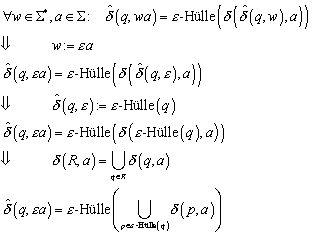
In klarer Sprache bedeutet das, dass angewendet auf ein einzelnes Symbol a (und einen Zustand q) nichts anderes ist, als die Vereinigung der Ergebnisse von für jeden einzelnen Zustand aus der e-Hülle von q. Die e-Hülle von q wiederum ist nichts anderes als eine Menge von Zuständen, zwischen denen der Automat indifferent ist. Genau dieses Verhalten ist auch die Forderung, die wir an die Übergangsfunktion des NFA stellen. Wir haben jetzt für den Sonderfall bewiesen, dass die Forderung, die wir an die „neue“ Funktion stellen, durch die „alte“ Funktion erfüllt werden.

Die Korrektheit für den Sonderfall , d.h. haben wir bereits bei der Definition der akzeptierenden Zustände unter verbal erklärt.

Für erbringen wir den Beweis induktiv. Da , lässt sich die Eingabe zerlegen in . Durch die Induktionsvoraussetzung gilt

Weiterhin gilt:

Aus und folgt:

Aus folgt unter Zuhilfenahme der Induktionsannahme[7]:

Mit dem Wissen von lässt sich wie folgt umschreiben:

Nach der Definition von (siehe gilt:

Damit folgt aus , und :

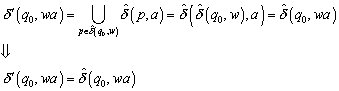
11 Vorlesung vom 11. Mai 2000

11.1 Äquivalenz von endlichen Automaten und regulären Ausdrücken

11.1.1 Von regulären Ausdrücken zu endlichen Automaten

In den vorangegangen Wochen haben wir verschiedene Typen von endlichen Automaten kennengelernt. Dabei haben wir gezeigt, dass deterministische und nichtdeterministische endliche Automaten (DFA und NFA) sowie nichtdeterministische Automaten mit e‑Übergängen die gleiche Klasse von Sprachen, die regulären Sprachen, beschreiben und beliebig ineinander konvertiert werden können.

Jetzt wollen wir zeigen, dass die Sprachen, die durch reguläre Ausdrücke definiert werden, ebenfalls äquivalent zu diesen endlichen Automaten sind. Diese Sprachen werden auch reguläre Mengen genannt (nach dem Satz von Kleene: „Die Menge der durch reguläre Ausdrücke beschreibbaren Sprachen ist genau die Menge der regulären Sprachen.“)

Folgendes Schaubild verdeutlicht den Zusammenhang und die Abhängigkeit zwischen regulären Ausdrücken und endlichen Automaten, die wir im Anschluß zeigen wollen.

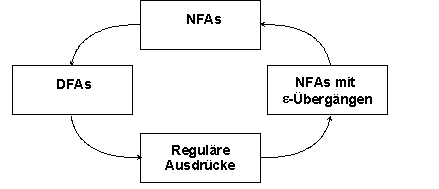
Abbildung 18 - Äquivalenzkreislauf reguläre Ausdrücke - endliche Automaten

Satz:

Sei r ein regulärer Ausdruck, dann existiert ein NFA mit e‑Übergängen, der die zum regulären Ausdruck gehörende Sprache L(r) akzeptiert.

Beweis

Für einfache reguläre Ausdrücke läßt sich die Behauptung einfach zeigen. Wenn r die leere Menge , das leere Wort oder ein einzelnes Zeichen ist, dann liegt ein einfacher regulärer Ausdruck vor.

Zu zeigen ist, dass ein solcher regulärer Ausdruck in einen endlichen Automaten mit e‑Übergängen überführt werden kann, wir konstruieren also einen solchen Automaten gemäß der Vorgabe des regulären Ausdrucks. Diese drei ein- oder keinelementigen Ausdrücke ohne Operator stellen gewissermaßen den Induktionsanfang der Induktion über die Anzahl der Operatoren des regulären Ausdrucks vor.

Wenn wir zeigen können, dass ein beliebiger regulärer Ausdruck mit beliebig vielen Operatoren n in einen NFA mit e‑Übergängen und einem einzigen Endzustand, aus dem keine Übergänge herausführen, überführt werden kann, dann existiert für jeden regulären Ausdruck ein entsprechender Automat und die Äquivalenz ist bewiesen.

Für die drei elementaren Zustände können folgende Automaten gebaut werden, die einen einzigen Endzustand haben, der erreicht wird, wenn ein Wort der Sprache L(r) erkannt wird und von dem keine Übergänge ausgehen.

Abbildung 19 - NFAs für reguläre Ausdrücke ohne Operatoren

Für einen regulären Ausdruck, der das leere Wort erkennt, geht der Automat direkt in den Endzustand über, da e‑Übergänge erlaubt sind. Der reguläre Ausdruck leere Menge tritt niemals in den Endzustand ein und der reguläre Ausdruck für ein bestimmtes Zeichen geht genau dann in den Endzustand über, wenn dieses Zeichen erkannt wird.

Für den Induktionsschritt von i - 1 auf i Operatoren lassen sich NFAs mit e‑Übergängen für reguläre Ausdrücke mit weniger als i Operatoren bereits konstruieren (i ³ 1). Dabei muß zwischen drei Verknüpfungsarten unterschieden werden

1. Vereinigung:

r = r₁ + r₂

2. Konkatenation:

r = r₁ · r₂

3. Kleensche Hülle:

r = r₁*

11.1.2 Vereinigung zweier regulärer Ausdrücke als NFAs

Gegeben sind zwei reguläre Ausdrücke r₁ und r₂ mit jeweils weniger als i Operatoren, die regulären Sprachen L(r₁) und L(r₂) beschreiben. Nach Induktionsannahme gibt es zwei entsprechende NFAs und , die diese Sprachen erkennen. Die beiden Automaten haben voneinander disjunkte Zustände, die unterschiedlich zu benennen sind, um sie in einer gemeinsamen Zustandmenge vereinigen zu können. Damit bilden wir einen neuen Automaten als Vereinigung von M₁ und M₂.

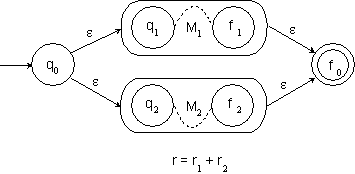
Abbildung 20 - Vereinigung von regulären Ausdrücken

Zu den Zuständen der beiden Automaten kommt ein gemeinsamer Startzustand q₀ und ein gemeinsamer Endzustand f₀, aus dem keine weiteren Übergänge herausführen. Die erzeugte reguläre Sprache L(r) soll entweder Wörter akzeptieren, die in L(r₁) oder in L(r₂) enthalten. Daher geht der konstruierte Automat beim Start von q₀ in einem e‑Übergang entweder in M₁ oder in M₂. Gemäß Induktionsannahme erkennt er dort ein entsprechendes Wort des jeweiligen Automaten und verläßt den Teilautomaten nicht, bevor er in den Endzustand f₁ bzw. f₂ eingetreten ist. In einem weiteren e‑Übergang geht der Automat vom Endzustand eines Teilautomaten in den gemeinsamen neuen Endzustand f₀.

Die Vereinigung zweier regulärer Ausdrücke, die sich in NFAs überführen lassen, liefert also wieder einen regulären Ausdruck, für den ein NFA existiert. Formal läßt sich der Automat, der L(r) erkennt als M ausdrücken:

Die Übergangsfunktion d ist folgendermaßen gestaltet:

Die Übergänge in den beiden Teilautomaten M₁ und M₂ entsprechen den Übergangsfunktionen d₁ und d₂. Dabei werden alle Zustände außer den beiden Endzuständen f₁ und f₂ betrachtet. Da f₁ und f₂ Endzustände von M₁ und M₂ sind, aus denen per Induktionsannahme keine Übergänge herausführen, können sie nicht in der folgenden Definition enthalten sein, sondern gehen gemäß obigem Abschnitt mit einem e‑Übergang zum gemeinsamen Endzustand f₀ über.

Somit gilt der Induktionsschritt für Vereinigung:

11.1.3 Schnitt zweier regulärer Ausdrücke als NFAs

Die Konkatenation zweier regulärer Ausdrücke r₁ und r₂ zu einem neuen regulären Ausdruck r gestaltet sich ähnlich. Seien M₁ und M₂ NFAs, die L(r₁) und L(r₂) akzeptieren, dann sei M ein Automat, der die Sprachen beider Automaten konkateniert.

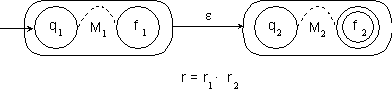
Abbildung 21 - Konkatenation von regulären Ausdrücken

Der Startzustand von M₁ ist gleichzeitig Startzustand von M. Der Automat durchläuft in M₁ die einzelnen Zustände, bis er ein Wort gemäß r₁ erkennt und in f₁ übergeht. In einem e‑Übergang geht der Automat von f₁ in q₂, den Startzustand von M₂, über. Hier tritt er über mögliche Zwischenzustände in f₂, den Endzustand von M₂, der auch gleichzeit Endzustand von M ist.

M akzeptiert also eine reguläre Sprache L(M), die gemäß Abschlußeigenschaften regulärer Sprachen aus der Konkatenation der per Induktionsannahme regulären Sprachen L(M₁) und L(M₂) entsteht. Für r existiert so ein NFA mit e‑Übergängen. Formal definiert sich M als:

Die Übergangsfunktion d für f₁ ist folgendermaßen gestaltet. Da f₁ Endzustand von M₁, führen keine Übergänge aus f₁ heraus, eine Verbindung zwischen M₁ und M₂ wird daher benötigt.

In den beiden Teilautomaten wird d entsprechend mit d₁ und d₂ definiert. Der Übergang von f₁ wurde bereits definiert, f₂ verhält sich wie in M₂ und ist gleichzeitig Endzustand von M.

Somit ist der Induktionsschritt für Konkatenation gezeigt:

11.1.4 Kleensche Hülle eines regulären Ausdruckes als NFA

Bei der Hüllenbildung (auch Stern genannt) über den regulären Ausdruck r₁ kann r₁einmal, keinmal oder beliebig oft auftreten. Dementsprechend führen wir einen Automaten M ein, der den zu r₁ passenden Automaten erweitert.

Tritt r₁ keinmal auf, so geht M vom neuen Startzustand q₀ in einem e‑Übergang direkt in den neuen Endzustand f₀ über. Andernfalls ist r₁ mindestens einmal vorhanden und M geht in den Bereich von M₁. Hier kann der reguläre Ausdruck beliebig oft wiederholt werden, da von f₁ mit einem e‑Übergang in q₁ verzweigt werden kann. Folgen keine weiteren Wiederholungen von r₁, geht M in einem weiteren e‑Übergang in den Endzustand f₀.

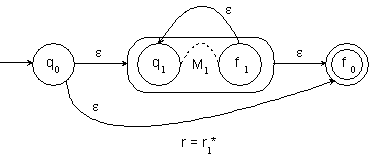
Abbildung 22 - Kleensche Hülle über regulärem Ausdruck

M akzeptiert somit reguläre Sprachen, die L(M) = L(M₁)* genügen und kann folgendermaßen definiert werden

Die zugehörige Übergangsfunktion d entspricht im Wesentlichen d₁, muß allerdings für die Sterneigenschaften erweitert werden

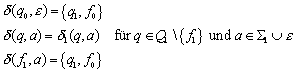
Somit ist der Induktionsschritt für die Kleensche Hülle (oder Stern) gezeigt. Es existiert ein NFA M, der beliebig viele Konkatenationen der von r₁ akzeptierten Sprache sowie das leere Wort akzeptiert.

Mit den drei Fällen Vereinigung, Konkatenation und Hüllenbildung ist die Induktion über die Anzahl der Operatoren abgeschlossen. Verschachtelte, vollständig geklammerte Ausdrücke können mit Hilfe der Abschlußeigenschaften in diese Grundformen zerlegt werden.

11.1.5 Beispiel: Konstruktion eines NFA mit e‑Übergängen für einen regulärem Ausdruck

Als Beispiel betrachten wir einen regulären Ausdruck r = 01*+1. Mit vollständiger Klammerung und Aufspaltung in die Operationen Vereinigung, Konkatenation und Stern sowie Substitution mit symbolischen Ausdrücken r_i (ihrerseits wieder reguläre Ausdrücke) erhält man

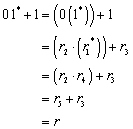
So zerlegt lassen sich für jeden Ausdruck r_i wie im vorangegangenen Abschnitt beschrieben Automaten konstruieren und diese dann zusammensetzen. Dabei beginnt man mit dem am weitesten in der Klammerhierarchie innenliegenden Ausdruck r₁ und erweitert den Automaten immer um weitere Zustände für die umgebenden Ausdrücke.

Für r₁ ist die Operation Stern anzuwenden, daher konstruiert man einen Automaten mit 4 Zuständen, einem Start- und einem Endzustand q₁ und q₄, sowie zwei weiteren Zuständen q₂ und q₃. Vom Startzustand q₁ kommt man in einem e‑Übergang zu q₂ oder direkt zum Endzustand q₄ (leeres Wort). Mit einer 1 kommt man zu q₃ und von dort per e‑Übergang zu q₂ zurück (Stern) oder zum Endzustand q₄.

Abbildung 23 - Automat für 1*

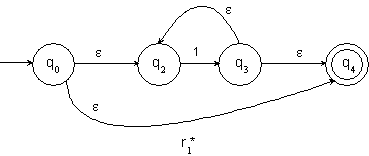
Die Konkatenation (Und) von r₂ und r₄ benötigt lediglich zwei weitere Zustände q₅ und q₆, die vor den Automaten für r₄ geschaltet werden. Von q₅ geht der Automat nur in q₆ über, wenn eine 0 als Zeichen anliegt. Von q₆ gelangt der Automat in einem e‑Übergang in q₀, den Anfangszustand des oben beschriebenen Automaten. Dadurch ergibt sich folgender Automat

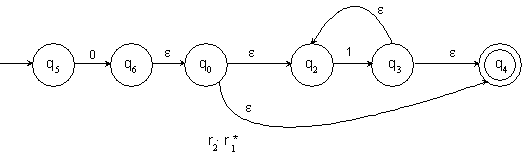
Abbildung 24 - Automat für 01*

Der noch verbleibende Ausdruck r₃ muß mit r₅ = r₂·r₁* in Vereinigung (Oder) aufgehen. Dazu benötigt man einen neuen Startzustand q₇ und einen neuen Endzustand q₈. Für die Konstruktion eines Automaten, der r₃ erkennt, benötigt man weitere zwei Zustände q₉ und q₁₀. Vom neuen Startzustand q₇ gehen e‑Übergänge zu den Startzuständen der beiden alternativen Automaten q₅ und q₉. Genauso gehen von den Endzuständen der Teilautomaten q₄ und q₁₀ e‑Übergänge zum neuen Endzustand q₉. Weiter tritt der Automat von q₉ bei Zeichen 1 in den Zustand q₁₀.

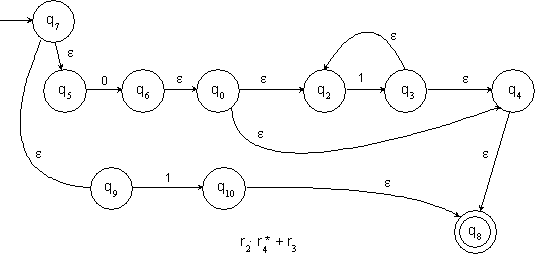
Abbildung 25 - Gesamter Automat

Für den regulären Ausdruck 01*+1 exisiert wie gezeigt ein endlicher, deterministischer Automat mit e‑Übergängen, der folgende Definition hat. Für die zehn Zustände gibt es einen Startzustand q₇ und einen Endzustand q₈. Die Übergangsfunktion entspricht dem oben aufgeführten Graphen für den gesamten Automaten.

Auf diese Weise lassen sich für alle regulären Ausdrücke DFAs und NFAs konstruieren, die die gleiche Sprache wieder reguläre Ausdruck erkennen.

11.1.6 Von endlichen Automaten zu regulären Ausdrücken

Gemäß der Darstellung des Schaubildes zu Beginn des Protokolls, haben wir gezeigt, das sich reguläre Ausdrücke in nichtdeterministische Automaten mit e‑Übergängen umwandeln lassen. Aus vorangegangenen Protokollen ist bekannt, dass DFAs, NFAs und NFAs mit e‑Übergängen äquivalent sind. Jetzt ist der Weg zurück zu den regulären Ausdrücken zu zeigen, der letzte Pfeil im Schaubild von DFAs zu regulären Ausdrücken.

Satz:

Wenn eine Sprache L von einem DFA akzeptiert wird, dann läßt sich diese Sprache L durch einen regulären Ausdruck r beschreiben.

Beweis

Es ist zu zeigen, dass der zu bestimmende reguläre Ausdruck r die gleiche Sprache beschreibt wie der gegebene Automat M, also gilt. Sei M ein endlich deterministischer Automat, dessen Zustände von 1 bis n durchnummeriert sind und q₁ der Startzustand ist.

seien Sprachen mit und , die wir durch reguläre Ausdrücke beschreiben wollen. enthält alle Wörter x, die den Automaten von Zustand q_i über verschiedene Zwischenzustände nach q_j überführen. Dabei seien q_l die besuchten Zustände[8] und es gelte l £ k für alle Wörter x.

Diese Sprachen R können rekursiv definiert und per Induktion über k bewiesen werden. Für k = 0 als Induktionsannahme geht der Automat direkt von Zustand q_i nach q_j ohne dabei Zwischenzustände zu besuchen, da kein Zustand q_p mit p £ 0 existiert. Für den Fall enthält die Sprache alle Zeichen, für die der Automat beginnend in q_i direkt in q_j übergeht.

Für den Fall, dass gegeben ist, erkennt der Automat alle Zeichen ohne über Zwischenzustände zu gehen, bei denen er von q_i in q_i geht, also im gleichen Zustand verbleibt. Im „Zustand Verbleiben“ heißt aber auch, dass der Automat keinen Zustandswechsel macht und so dass leere Wort zur Sprache gehört

Für diese Fälle ist eine endliche Menge von Zeichen und ein regulärer Ausdruck läßt sich aufstellen. Die Induktionsannahme ist damit bewiesen. Ein entsprechender regulärer Ausdruck besteht aus der Veroderung der auftretenden Zeichen sowie dem leeren Wort, falls

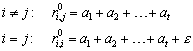
Für den Induktionsschritt von k auf k+1 verwenden wir die Rekursionsgleichung und setzen als gegeben voraus.

Wörter x, bei denen der Automat von q_i nach q_j übergeht, müssen den Zustand q_k+1 nicht passieren. Dann wird dieser Zustand nicht benötigt und die Sprache läßt sich durch das bereits bewiesene ausdrücken. Wird der Zustand benötigt, geht der Automat von q_i in q_k+1 über und kann innerhalb von q_k+1 beliebig oft aufgerufen werden (Stern, Kleensche Hülle). Anschließend tritt er in q_j ein und erkennt somit Wörter, bei denen der Automat durch q_k+1 als Zwischenzustand geht.

Ein entsprechender regulärer Ausdruck für die Sprache läßt sich aufstellen, da die Rekursionsgleichung nur die Operationen für reguläre Ausdrücke Vereinigung, Konkatenation und Hüllenbildung enthält. Nach Induktionsannahme beschreiben die regulären Ausdrücke für k bereits reguläre Sprachen. Die Anwendung der Operationen auf regulären Ausdrücke ergibt wieder reguläre Ausdrücke genauso wie die Anwendung der Operationen auf reguläre Sprachen wieder eine reguläre Sprache ergibt (siehe Abschlußeigenschaften). Damit läßt sich der folgende reguläre Ausdruck aufstellen

Der Induktionsschritt ist damit bewiesen und es lassen sich beliebige reguläre Ausdrücke aufstellen, die Teilmengen von L(M) beschreiben. Für dem Automaten M betrachten wir jetzt alle Wörter, die den Automaten vom Startzustand q₁ in einen Endzustand q_i überführen und dabei alle n Zustände des Automaten (siehe Definition am Anfang des Beweises) besuchen. Die Menge dieser Wörter ist die Sprache, die der Automat erkennt.

Damit läßt sich analog zum vorangeganen Abschnitt ein regulärer Ausdruck konstruieren und so der Beweis abschließen. Für die möglichen Endzustände

verwenden wir die Indizes i₁,i₂,...,i_p. Der reguläre Ausdruck ist so die Veroderung regulärer Ausdrücke, die die Wörter beschreiben, bei denen der Automat in jeweils einem gemeinsamen Endzustand hält.

Somit wurde wurde gezeigt, dass man zu einer von einem DFA M akzeptierten Sprache L(M) einen regulären Ausdruck r angeben kann, der die gleiche reguläre Sprache L(r) = L(M) beschreibt.

Reguläre Ausdrücke, endliche deterministische, endliche nichtdeterministische sowie endliche nichtdeterministische Automaten mit e-Übergängen sind somit wie im heutigen und den vorangegangen Protokollen gezeigt, äquivalent und beschreiben die Menge der regulären Sprachen.

12 Vorlesung vom 16. Mai 2000

12.1 Wiederholung der letzten Vorlesung

12.1.1 Abschlusseigenschaften

Für die folgenden Sprachen soll überprüft werden, ob sie zur Klasse der regulären Sprachen gehören.

Beispiel 1

Wir wissen, dass die Sprache nicht regulär ist, folgt daraus, dass die Sprache auch nicht regulär ist? Der argumentative Beweis nach Myhill-Nerode sieht wie folgt aus:

Es ist nun zu zeigen, dass der unendlich ist. Dies ist aber leicht zu sehen, wenn man die Wörter der Sprache, als Zusammensetzung aus und für alle sieht. Es ist Fakt, dass es unendlich viele Wörter gibt. Somit ist der Index unendlich und damit .

Beispiel 2

Nun ist die Frage, ob auch die Rückrichtung gilt. In anderen Worten gilt:

Nehmen wir an sei regulär. Sei weiterhin ein Homomorphismus, welcher die folgenden Abbildungen durchführt:

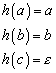
Bildet man nun die Sprache:

und vereinigt diese mit beliebigen Folgen der Form so ergibt sich die Sprache:

Diese wäre aufgrund der Abgeschlossenheit der Regulären Sprachen immer noch regulär. Jedoch kann man diese Sprache auch umformulieren zu:

Jedoch wissen wir, von unserer Annahme, sei regulär, dass diese falsch ist. Somit kann auch die Sprache nicht regulär sein.

Beispiel 3:

Man kann weiterhin zeigen, dass gilt:

Angenommen die Sprache wäre regulär, dann wäre auch die Sprache

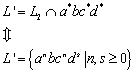
regulär. Nun kann man einen Homomorphismus verwenden mit den Abbildungen:

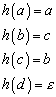
Sei nun die Sprache, welche erzeugt wird, indem man den Homomorphismus auf die Sprache anwendet:

Diese müsste auch regulär sein, da wir jeweils nur strukturerhaltende Operationen verwendet haben. Wir wissen jedoch, dass die Sprache bestehend aus Wörtern der Form nicht regulär somit ergibt sich ein Widerspruch.

Beispiel 4:

Gilt:

Angenommen, dass regulär ist, dann ist auch die Sprache:

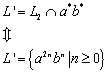
regulär. Wieder definieren wir einen Homomorphismus mit den Abbildungen:

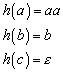
Sei nun die Sprache, welche erzeugt wird, indem man den inversen Homomorphismus auf die Sprache anwendet:

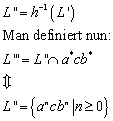
Diese müsste auch regulär sein, da wir jeweils wieder nur strukturerhaltende Operationen verwendet haben. Wir wissen jedoch, dass die Sprache bestehend aus Wörtern der Form nicht regulär somit ergibt sich ein Widerspruch.

Beispiel 5:

Zum Schluss gilt noch zu überprüfen, ob:

Wieder nehmen wir zunächst an, dass die Sprache regulär sei. Dann ist auch die Sprache:

regulär. Durch Konkatenation bilden wir:

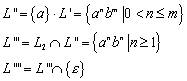
Dann sind . Doch wiederum gilt, da die Sprache nicht regulär ist, dass auch nicht regulär ist.

12.2 Beispiel zur Umwandlung eines Automaten dem entsprechenden Regulären Ausdruck

In diesem Abschnitt beschäftigen wir uns hauptsächlich mit dem folgenden Automaten:

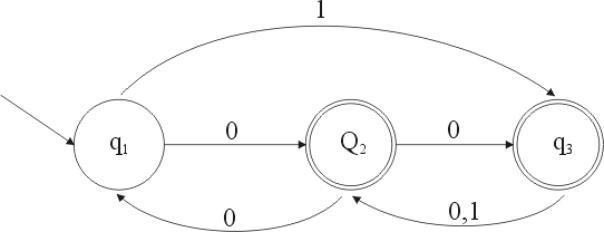
Abbildung 26: der endliche Automat des Beispiels

k=0	k=1	k=2

Sei der abgebildete endliche Automat. Die Wert sind in Tabelle 1 abgebildet. Dabei wurden die regulären Ausdrücke vereinfacht, und zwar in der Form: oder . Zum Beispiel ergibt sich für :

Ebenso ist:

Bedenkt man, dass und weiterhin gilt , dann ist:

Da weiterhin der Ausdruck äquivalent zu ist, ergibt sich für zunächst und schließlich . Die Regulären Ausdrucke für ergeben sich aus den akzeptierenden Zuständen. Also ist zu bestimmen. Mit:

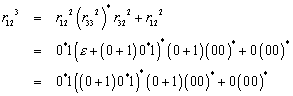
und

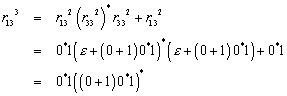
ergibt sich dann:

Dies stellt den Regulären Ausdruck für den Beispielautomaten dar.

12.3 Endliche 2-Wege Automaten

Dieser Abschnitt dient nur zur Information, da diese Automaten kein Thema dieser Vorlesung sein sollen. Deterministische endliche Zweiwegautomaten sind definiert als Quintupel unterschiedlich zum „normalen“ DFA ist hier zum einem dass die Übergangsfunktion neben einem Zustand noch eine Laufrichtung zurückgibt, in welcher der nächste Zustand besucht werden soll. ist also auf definiert. Es kann jedoch gezeigt werden, das ein und zwei-Wege endliche Automaten gleichwertig sind.

13 Vorlesung vom 23. Mai 2000

13.1 Grammatiken

13.1.1 Beispiel zu Grammatiken

Als Beispiel für eine Grammatik diene hier die Menge der booleschen Ausdrücke[9]. Das Startsymbol ist ein Nicht-Terminalsymbol, das wir „BOOL“ nennen. Als Terminalsymbole lassen wir alle Zeichen zu, die man gemeinhin für boolesche Ausdrücke verwendet. Die Produktionsregeln sind zu entnehmen, und sollten jeden booleschen Ausdruck produzieren können:

Der Ableitungsbaum eines beispielhaften booleschen Ausdruckes gemäß obiger Grammatik könnte wie folgt aussehen:

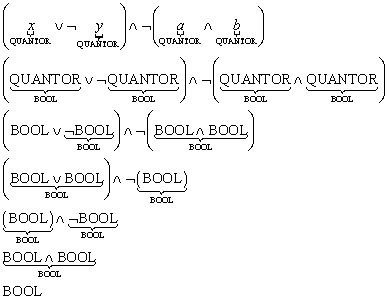
Wie man sieht, beginnt die Transformation bei einem gewöhnlichen booleschen Ausdruck, und endet bei dem Startsymbol S[10].

13.2 Die Äquivalenz von regulären Grammatiken und endlichen Automaten

Satz:

Sei eine Sprache, dann gilt:

Beweis:

1 Þ 2:

Gegeben sei der endliche Automat

Wir definieren eine neue Grammatik, die dem endlichen Automaten M entsprechen soll. Diese neue Grammatik benutzt das Alphabet des Automaten als Terminalalphabet, und die Zustandsmenge des Automaten als Nicht-Terminalalphabet:

Es bleibt die Frage nach der Produktionsmenge P.

Wir zeigen nun, dass die durch G’ definierte Menge tatsächlich die Menge ist, die von M akzeptiert wird. Für jedes Wort, das der Automat M akzeptiert, gilt:

Aus folgt:

Aus und folgt:

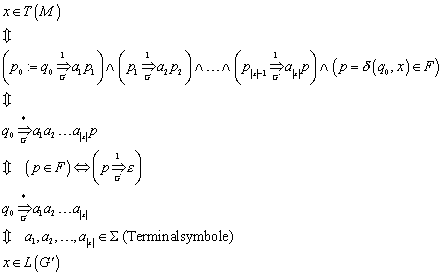
Die Mengen sind also identisch:

„Ü“:

Gegeben sei die reguläre Grammatik

Wir definieren einen nichtdeterministischen, endlichen Automaten M’, welcher der regulären Grammatik entsprechen soll. Dieser neue Automat benutzt die Nicht-Terminalsymbole der Grammatik als Zustandsmenge, und die Terminalsymbole der Grammatik als Eingabealphabet. Wir definieren weiterhin den ausgezeichneten (akzeptierenden) Zustand f:

Die Menge der akzeptierenden Zustände F seien alle jenen Zustände (bzw. Nicht-Terminalsymbole), welche in das leere Wort übergehen können, sowie der ausgezeichnete Zustand f[11]:

Die Übergangsfunktion ist beim endlichen Automaten definiert auf dem Kreuzprodukt von Zustandsmenge und Eingabesymbol, d.h. in unserem Fall, auf dem Kreuzprodukt der Nicht-Terminalsymbole (plus „f“) und der Terminalsymbole. Die Übergangsfunktion liefert beim endlichen Automaten eine Teilmenge der Zustandsmenge zurück, d.h. in unserem Fall eine Teilmenge der Nicht-Terminalsymbole.

Für jeden Zustand, der einem Nicht-Terminalsymbol entspricht, welches direkt in ein Terminalsymbol übergehen kann (), soll der neue Automat (unter anderem) in den ausgezeichnete Zustand f übergehen:

Wir zeigen nun, äquivalent zum ersten Teil des Beweises, dass die von M’ akzeptierte Menge tatsächlich die Menge ist, die durch G definiert wird[12]. Für jedes Wort, das unser neuer Automat M’ akzeptiert, gilt:

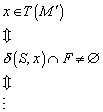
Falls einen Zustand Q’ beinhaltet, der akzeptierend ist, so gilt gemäß :

Bis hierher haben wir Umformungen vorgenommen, die eine Aussage darüber machen, wann ein Wort vom neuen Automaten akzeptiert wird, und wann nicht; in Abhängigkeit von dem Wort. Wie man an sieht, gibt es genau zwei Möglichkeiten, warum ein Wort von dem neuen Automaten akzeptiert werden kann – von diesen zwei Möglichkeiten muss mindestens eine Möglichkeit eintreten.

Die Definition des neuen Automaten und seiner Übergangsfunktion beruht auf einzelnen Symbolen, nicht auf Wörtern. Daher zerpflücken wir an dieser Stelle die Bearbeitung eines Wortes in die Bearbeitung vieler Symbole:

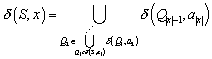
Mit diesem Wissen lässt sich umschreiben zu:

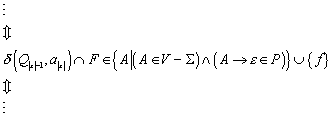
Auch bis hierher haben wir „nichts anderes“, als eine Gleichung, die beschreibt, wann ein Eingabewort von unserem neuen Automaten akzeptiert wird, und wann nicht – jetzt aber nur noch in Abhängigkeit von dem letzten Symbol des Eingabewortes, sowie dem Zustand des Automaten zu diesem Zeitpunkt.

Wir haben den ausgezeichneten Zustand f genau so definiert, dass ein Übergang f ergibt, falls der ursprüngliche Zustand gemäß Grammatik in das Eingabesymbol übergehen kann (siehe ):

Mit diesem Wissen folgt:

Die obige, boolesche „Kürzung“ durften wir vornehmen, da diese Bedingung gemäß der Definition der Übergangsfunktion immer erfüllt ist. Es gilt nun, irgendwie den „Weg zurück“ zu finden vom Zustand zum Zustand S. Aus folgt:

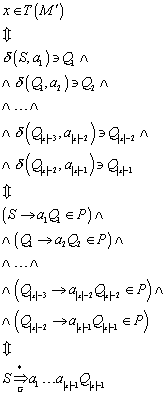
Oho. Wir wissen nun also, dass – falls ein Wort von unserem neuen Automaten akzeptiert wird, das zugehörige Nicht-Terminalsymbol Bestandteil der durch die Grammatik definierten Sprache ist. Weiterhin wissen wir aus , dass der „letzte Zustand“ des Automaten in ein Terminalsymbol übergeht. Daraus folgt:

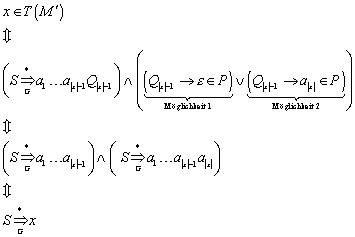
Die Mengen sind also identisch:

13.3 Die Sprache „aⁿbⁿ“

Satz:

Die Sprache ist nicht regulär!

Beweis:

Wir führen einen Widerspruchsbeweis durch, und behaupten, L ist regulär. Dann existiert auch ein endlicher Automat M, welcher L akzeptiert:

Wir gehen davon aus, dass dieser Automat existiert und funktioniert. Wir betrachten diesen Automaten nach der „Hälfte“ der Ausführungszeit, d.h. zu dem Zeitpunkt, an dem er die a’s abgearbeitet hat, und die b’s noch nicht. Wir wählen ein Eingabewort, dass genau so viele a’s enthält, wie der Automat Zustände besitzt. Nach der Verarbeitung aller a’s befindet sich der Automat in einem Zustand, den wir q nennen:

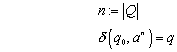
Der Automat ist in dem Startzustand q₀ gestartet, hat n Eingabezeichen verarbeitet, und hat demzufolge n mal seinen Zustand gewechselt. Außer dem Startzustand q₀ existieren noch (n-1) weitere Zustände. Daraus folgt, dass der Automat mindestens einen Zustand mehr als einmal angenommen hat:

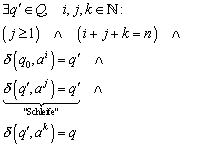
Für den Automaten ist es logischerweise „egal“, ob er die Schleife ausführt, oder nicht. Daraus folgt, dass der Automat zwischen den beiden Eingabewörtern aⁱ und a^i+j indifferent ist:

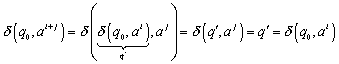
Das bedeutet ganz allgemein, dass man die Schleife auch weglassen kann, d.h. die a^j’s aus dem Eingabewort weglassen kann, ohne dass sich am Verhalten des Automaten irgendetwas ändert:

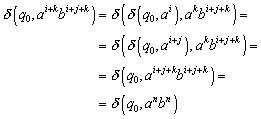
Wir haben durch definiert, dass Eingabewörter der Form aⁿbⁿ von dem Automaten akzeptiert werden, d.h. den Automaten vom Startzustand aus in einen akzeptierenden Zustand versetzen. Das gleiche Verhalten gilt demnach für Eingabewörter der Form a^i+kb^i+j+k, mit j>0:

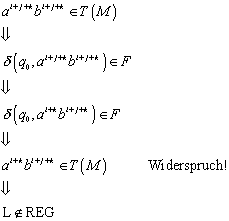
Unser Automat akzeptiert demzufolge auch Eingabewörter der Form a^i+kb^i+j+k, welche aber nicht Bestandteil der gegebenen Sprache L sind. Die Sprache L ist nicht regulär!

13.4 Das Pumping-Lemma

Satz:

„Wenn man einen Automaten hat, und ein akzeptiertes Wort kennt, dessen Länge größer ist als die Anzahl der Zustände des Automaten, dann ist die durch den Automaten akzeptierte Sprache unendlich.“

Wir haben im vorangegangenen Beispiel gesehen, dass es einen Zusammenhang gibt, zwischen der Anzahl von Zuständen eines Automaten, der Länge eines Wortes der erzeugten Sprache, und der Anzahl der Zustandsschleifen während der Verarbeitung dieses Wortes.

Das Pumping-Lemma generalisiert diese Erkenntnis: Nach dem Pumping-Lemma gibt es für jede Sprache L eine bestimmte Wortlänge n, ab welcher Wörter, die in der Sprache enthalten sind, zwangsweise solche „Schleifen“ enthalten:

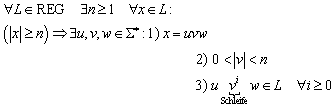
Beweis:

Der Beweis verläuft ähnlich wie im vorangegangenen Beispiel. Wenn L regulär ist, existiert auch ein endlicher Automat M, welcher L akzeptiert:

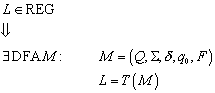
Wir dürfen davon ausgehen, dass dieser Automat existiert, und dass er eine endlich Zustandsmenge besitzt:

Angenommen, es existiert ein Eingabewort, welches von dem Automaten akzeptiert wird, und welches genauso viele Buchstaben besitzt, wie der Automat Zustände hat. Dann startet der Automat in dem Startzustand q₀, verarbeitet n Eingabezeichen, und wechselt demzufolge n mal seinen Zustand. Außer dem Startzustand q₀ existieren noch (n-1) weitere Zustände. Daraus folgt, dass der Automat mindestens einen Zustand mehr als einmal annimmt:

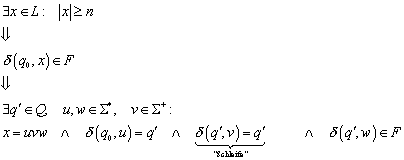
Für den Automaten ist es logischerweise „egal“, ob, und wie oft er die Schleife ausführt. Daraus folgt, dass der Automat zwischen den Eingabewörtern der Form wvⁱw für i>0 indifferent ist:

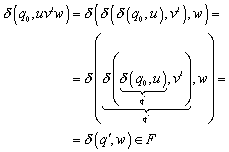
Daraus folgt:

13.5 Entscheidbarkeit

13.5.1 Prädikate

Der Begriff des „Prädikates“ ist der Prädikatenlogik als Teilgebiet der mathematischen Logik entnommen. Ein Prädikat ist eine Aussage, die entweder wahr oder falsch ist. Ein Prädikat wird zumeist als mathematische Funktion definiert.

13.5.2 Definition der Entscheidbarkeit

Sei S eine Menge, und ein Prädikat mit

Es gilt:

Entscheidbar sind z.B. folgende Fragen:

1. T(M)=Æ ?

2. T(M) endlich?

3. T(M) unendlich?

Die Beweise dafür erbringen wir im Folgenden.

13.5.3 Beispiel: Entscheidbarkeit der leeren Sprache

Behauptung:

Die Frage, ob T(M)=Æ, ist entscheidbar.

Beweis:

Sei , . Es gilt:

Wieso?

„Hinrichtung“:

Diese Richtung ist trivial. Wenn der Automat überhaupt kein einziges Wort akzeptiert, dann erst recht keines, das eine bestimmte Länge hat.

Rückrichtung:

Hierfür bemühen wir einen Widerspruchsbeweis. Wir nehmen an, dass der Automat alle Wörter der beschriebenen Länge nicht akzeptiert, aber es trotzdem Wörter gibt, die der Automat existiert:

Annahme:

Wir betrachten nun das kürzeste dieser akzeptierten Wörter, und nennen es x:

Gemäß Annahme gilt für die Länge dieses Wortes:

Nach dem Pumping-Lemma gilt, dass dieses Wort in dem endlichen Automaten „Schleifen“ verursachen muss:

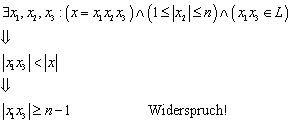
Das bedeutet, dass es automatisch auch ein Wort geben müsste, welches ebenfalls akzeptiert wird, aber gegen die Annahme verstößt. Also gilt , und damit gilt:

13.5.4 Beispiel: Entscheidbarkeit der unendlichen Sprache

Behauptung:

Die Frage, ob T(M) unendlich ist, ist entscheidbar.

Beweis:

Sei ein DFA, . Es gilt:

Wieso?

Rückrichtung:

Wenn ein Wort von dem Automaten akzeptiert wird, und genauso viele oder mehr Buchstaben besitzt, wie der Automat Zustände, dann ist gemäß dem Pumping-Lemma eine Schleife in dem Automatenablauf, die „aufgeblasen werden kann“:

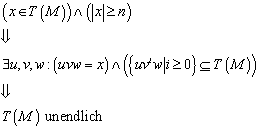
„Hinrichtung“:

Wir gehen von der Menge aller Wörter aus, die von dem Automaten akzeptiert werden, und länger sind als 2n-1. Falls diese Menge leer ist, bedeutet das, dass die erzeugte Sprache ohnehin nicht unendlich sein kann. Wir gehen davon aus, dass diese Menge nicht leer ist. Aus dieser Menge greifen wir uns dann eines der kürzesten Wörter heraus, und nennen es y:

Da dieses Wort immer noch mehr Buchstaben besitzt, als der Automat Zustände, schlägt das Pumping-Lemma zu, und wir können eine „Schleife“ aus diesem Wort entfernen:

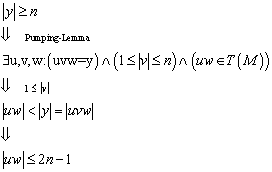
Damit haben wir schon die halbe Miete. Wir wissen nun, dass es automatisch ein akzeptiertes Wort geben muss, welches eine Länge kleiner oder gleich 2n-1 besitzt. Nun gilt es noch zu zeigen, dass dieses Wort auch eine Länge von größer oder gleich n besitzt:

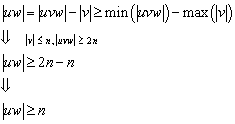
Damit ist der Beweis vollbracht. Es gilt also:

Also gilt , und daraus folgt:

13.5.5 Beispiel: Entscheidbarkeit der endlichen Sprache

Behauptung:

Die Frage, ob T(M) endlich ist, ist entscheidbar.

Beweis:

Somit gilt:

13.5.6 Beispiel: Entscheidbarkeit der Schnittmenge

Behauptung:

Die Frage, ob für zwei beliebige, endliche Automaten M₁ und M₂ gilt, ist entscheidbar.

Beweis:

Es ist bekannt, dass die Schnittmenge zweier regulärer Automaten (bzw. Mengen) wieder regulär ist:

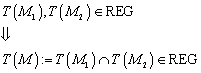
Wir haben bereits bewiesen, dass es für einen einzelnen Automaten entscheidbar ist, ob er eine leere Sprache akzeptiert, oder nicht:

13.5.7 Beispiel: Entscheidbarkeit der Teilmenge

Behauptung:

Die Frage, ob für zwei beliebige, endliche Automaten M₁ und M₂ gilt, ist entscheidbar.

Beweis:

Wir führen den Beweis über eine weitere Behauptung, die wir zuerst beweisen:

Behauptung a:

Beweis a:

„Hinrichtung“:

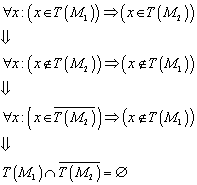
Rückrichtung:

Beweis über Contraposition (Ø Þ Ø):

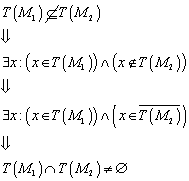
Also gilt die Behauptung a! Weiter im Beweis...

Wir konstruieren uns gedanklich einen dritten Automaten:

Unter Zuhilfenahme von folgt daraus:

Wir haben aber bereits in „13.5.6 Beispiel: Entscheidbarkeit der Schnittmenge“ gezeigt, dass die Frage, ob die Schnittmenge der durch zwei endliche Automaten definierten Sprachen nicht leer ist, entscheidbar ist. Damit ist der Beweis erbracht:

13.5.8 Beispiel: Entscheidbarkeit der Äquivalenz

Behauptung:

Die Frage, ob für zwei beliebige, endliche Automaten M₁ und M₂ gilt, ist entscheidbar.

Beweis a:

Wir können den Beweis nun auf bereits Bewiesenes zurückführen:

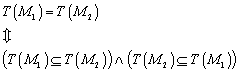
Den Beweis, dass dieser Zusammenhang entscheidbar ist, haben wir in „13.5.7 Beispiel: Entscheidbarkeit der Teilmenge“ erbracht. Daraus folgt:

Beweis b:

Wir konstruieren uns zwei minimale Automaten, die äquivalent zu den beiden gegebenen Automaten sind. Dann gilt:

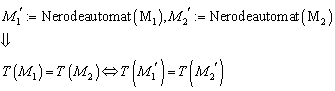
Vorausgesetzt, dass die beiden Automaten wirklich die selbe Sprache definieren, müssen die dazugehörigen Nerode-Automaten isomorph sein, d.h.:

Es ist nun möglich, alle denkbaren Abbildungen von nach auszuprobieren, und festzustellen, ob eine davon ein Isomorphismus ist. Es kann kein Isomorphismus dabei sein, wenn die Automaten nicht identisch sind... Auch hieraus folgt:

13.6 Kontext-freie Grammatiken

Definition:

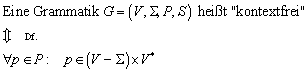
Im Gegensatz zur normalen Grammatik stehen hier auf „der linken Seite“ der Produktionen also lediglich Nicht-Terminalsymbole, und auch immer nur eines davon. Bei der normalen Grammatik standen hier auch Terminalsymbole, und dazu noch beliebig viele (konkateniert).

13.6.1 Beispiel zur Kontext-freien Grammatik

Gegeben sei die Grammatik:

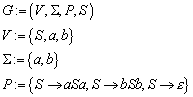
Behauptung:

„R“ bedeutet in diesem Zusammenhang das „umgedrehte Wort“. Die Grammatik beschreibt also Palyndrome.

Beweis:

Wir führen den Beweis mittels vollständiger Induktion über die Länge der Produktionen durch.

Induktionsbehauptung:

Induktionsverankerung (n=1):

„Hinrichtung“:

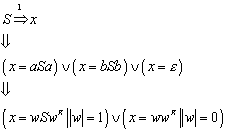
Rückrichtung:

Fallunterscheidung, Fall 1:

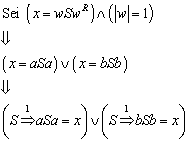
Fallunterscheidung, Fall 2:

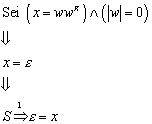
Induktionsschritt (n®n+1):

„Hinrichtung“:

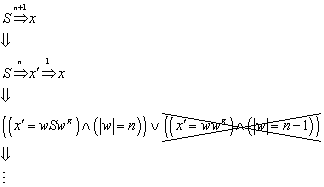
Die „Kürzung“ in dem obigen Ausdruck ist erlaubt, bzw. muss sogar sein, weil in diesem Fall kein Nicht-Terminalsymbol (d.h. S) mehr in dem Wort enthalten wäre. Es gäbe keine Produktion, die es erlauben würde, das Wort noch weiter zu verändern.

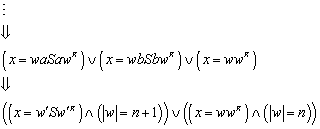
Rückrichtung:

Fallunterscheidung, Fall 1:

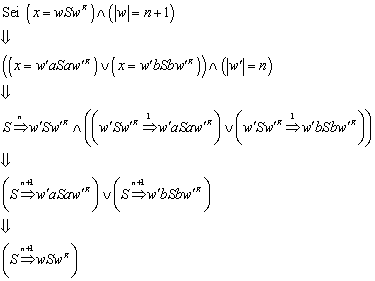
Fallunterscheidung, Fall 2:

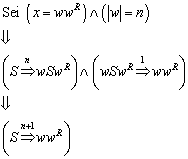
14 Vorlesung vom 25. Mai 2000

14.1 Ableitungen von Wörtern in kontextfreien Grammatiken

14.1.1 Ableitungen

Durch Ableitungen auf einer kontextfreien Grammatik formt man Nichtterminalsymbole in einem oder mehreren Ableitungsschritten auf Konkatenationen von Terminal- und Nichtterminalsymbolen um. Diesen Vorgang wollen wir näher betrachten.

Sei eine Grammtik, dann wir eine Sprache L(G), die von dieser Grammatik generiert wird. Hier und im Folgenden sei V die Menge der Nichtterminalsymbole und S die Menge der Terminalsymbole. Die Produktionen P dieser Grammatik wandeln (auch resubstitiuieren, ersetzen) Nichtterminalsymbole A in Folgen von Nichtterminal- und Terminalsymbolen um.

Eine Produktion aus P: angewandt auf mit liefert

Damit ist eine Relation auf der Menge der vereingten Terminal- und Nichtterminalsymbole und bezeichnet die Anwendung einer einzelnen Produktion. Die Anzahl der angewandten Produktionen, d. h. die Ableitungsschritte, kann über den Doppelpfeil geschrieben werden. Erfolgt die Ableitung der linken auf die rechte Seite in n Schritten, schreibt man entsprechend ein n über den Doppelpfeil.

Bildet man den transitiven Abschluß (transitive Hülle) der Relation, so bedeutet das die Ableitung über alle möglichen Schritte bis keine weiteren Ableitungen mehr möglich sind.

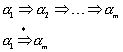
Reflexivität gilt, da dies dem Anwenden keiner Produktion auf ein Nichtterminalsymbol entspricht. Es gilt somit immer

Mit dieser Relation als Hilfsmittel zur Beschreibung von Ableitungen läßt sich die von der Grammatik G generierte Sprache L(G) beschreiben

Die Sprache L(G) besteht aus Zeichenketten, die nur Terminalsymbole () enthalten und durch beliebig viele Ableitungsschritte ausgehend vom Startsymbol S erzeugt () werden. Hierzu drei Anmerkungen

1. Eine Sprache ist kontextfrei, wenn sie von einer kontextfreien Grammatik erzeugt wird.

2. Während Zeichenketten bestehend aus Terminalsymbolen (Alphabet) Wörter der Sprache genannt werden, heißen die Zwischenschritte der Ableitung bestehend aus Nichtterminal- und - wenn nötig - Terminalsymbolen Satzform.

3. Zwei Grammatiken G₁, G₂ sind äquivalent, wenn sie dieselbe Sprache generieren ( L(G₁) = L(G₂) ).

14.1.2 Ableitungsbäume

Ableitungen lassen sich mit Ableitungsbäumen (auch Parse-Bäume genannt) visualisieren. Jede kontextfreie Grammatik kann mit Ableitungsbäumen beschrieben werden. Die Knoten solcher Bäume sind Terminal- und Nichtterminalsymbole. Die Wurzel ist immer ein Nichtterminalsymbol, während Terminalsymbole nur in Blättern auftreten. Betrachtet man den gesamten Ableitungsbaum, ist die Wurzel das Startsymbol der Grammatik.

Teilbäume eines Ableitungsbaumes sind Bäume mit einem Nichtterminalsymbol A als Wurzel und allen sich daraus ergebenden Kinderknoten. Die Anzahl der Knoten ist kleiner als die des gesamten zugrundliegenden Baumes, erseidenn der Teilbaum ist gleich dem Ableitungsbaum. Solche Teilbäume werden nach ihrer Wurzel genannt. Heißt die Wurzel also A spricht man von einem A-Baum.

Damit läßt sich jede Produktion einer Grammatik als Teilbaum beginnend mit der linken Seite als Wurzel und den 1 bis n Symbolen der rechten Seite als Kinderknoten darstellen. Die Symbole der rechten Seite seien abgekürzt mit

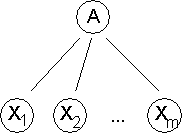
Abbildung 27 - Ableitungsbaum einer Produktion

Für einen Ableitungsbaum einer Grammatik gelten folgende Regeln

1. Jeder Knoten repräsentiert ein Symbol .

2. Die Wurzel stellt das Startsymbol der Grammatik dar.

3. Alle inneren Knoten sind Nichtterminalsymbole, da kontexfreie Grammatiken nur solche auf der linken Seite der Produktionen stehen haben. Entsprechend sind alle Terminalsymbole Blätter, aber nicht notwendigerweise alle Blätter Terminalsymbole.

4. Wenn ein Knoten ein Nichtterminalsymbol A repräsentiert und die Kinderknoten X₁, X₂,...X_m hat, dann gibt es eine Produktion aus der Menge der Produktionen von G mit (siehe Grafik vorangegangener Absatz).

5. Knoten, die das leere Wort e repräsentieren, sind immer Blatt, da sie das einzige Kind eines Knoten mit Nichtterminalsymbol darstellen (sogenannte e-Produktionen, wie wir später sehen werde). Aus dem leeren Wort können keine Abbildungen erfolgen und es kann ausschließlich auf das leere Wort und nicht auf Konkatenationen mit dem leeren Wort abgebildet werden, da sonst die restlichen Symbole der rechten Seite und nicht das leere Wort die Kinderknoten darstellen würden.

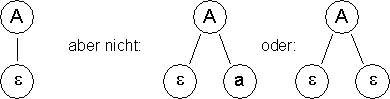
Abbildung 28 - richtige und falsche Ableitungsbäume von e-Produktionen

14.1.3 Beispiel für einen Ableitungsbaum

Gegeben sei eine Grammtik

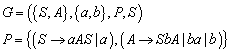
Das erste und letzte Zeichen der Wörter der zugehörigen Sprache sind also immer a. In der Mitte können b und a in mehrfacher Ausführung auftreten. Für das Wort

kann man folgende Ableitung mit dem entsprechenden Ableitungsbaum angeben.

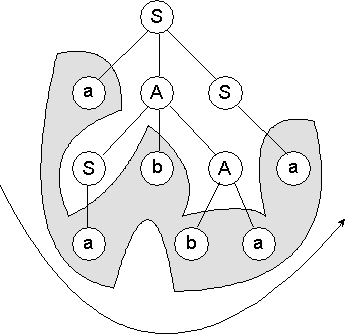
Abbildung 29 - Beispiel Ableitungsbaum für Wort aabbaa

Als „yield“ oder „Front“ bezeichnet man die Zeichenkette, die sich ergibt, wenn man die Blätter des Baumes perorder von links nach rechts abliest. In diesem Beispiel ist die Front das Wort aabbaa, es muß sich aber nicht ausschließlich um Terminalsymbole handeln, auch Nichtterminalsymbole sind je nach Grammatik möglich (bei Grammatiken, bei denen Blätter auch Nichtterminalsymbole sein können).

14.1.4 Die Beziehung zwischen Ableitungsbäumen und Grammatiken

Die Zusammenhänge zwischen Ableitungsbäumen und Ableitungen wurden im vorangegangenen Abschnitt nur exemplarisch und beschreibend dargelegt. Dies kann auch formal geschehen, wie im Folgenden gezeigt wird. Dazu wird wieder auf die Pfeilrelation zur Darstellung der Abbildungen und insbesondere auf die transitive Hülle dieser Relation zurückgegriffen.

Satz:

Für eine kontextfreie Grammatik gilt genau dann, wenn ein Ableitungsbaum für G mit der Front (yield) a existiert.

Beweis:

Da eine Û Beziehung vorliegt, muß in beide Richtungen bewiesen werden, was sich hier aber sehr ähnlich gestaltet. Zunächst die

„Hinrichtung“

Geht man von einem Baum aus und will damit die Ableitungsschritte zeigen, so beweist man per Induktion über die Anzahl der inneren Knoten. Anstatt des gesamten Ableitungsbaums vom Startsymbol S aus, wählen wir eine Ableitung der Form

von einem beliebigen Nichtterminalsymbol A zur Front a aus.

Induktionsverankerung (Anzahl innerer Knoten = 1)

Es handelt sich um eine einzelne Produktion aus G. Aus dem inneren Knoten A folgen n verschiedene Terminal- und Nichtterminalsymbole X₁,X₂,...,X_n als Front des Ableitungsbaumes. Die bereits weiter oben verwendete und hier nochmals abgebildete Grafik verdeutlich dies

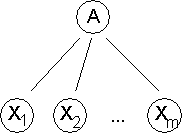
Abbildung 30 - Ableitung bei einem einzelnen inneren Knoten

Formal ausgedrückt ist der Satz für die Hinrichtung bei einem inneren Knoten bewiesen

Induktionsschritt:

Gelte die Behauptung nun für Teilbäume mit k - 1 inneren Knoten und sei a die Front eines A‑Baums mit k inneren Knoten (k > 1). Die Kinderknoten eines solchen Wurzelementes A können nicht alle Blätter sein, da wegen k größer eins mindestens ein Kinderknoten innerer Knoten (bzw. Nichtterminalsymbol) ist.

Die Kinderknoten seien von 1 bis n durchnummeriert und mit X₁,X₂,...,X_m bezeichnet. Dies entspricht wieder einer Produktion der Grammatik

Wegen k größer eins ist eines der X_i Nichtterminalsymbol. Von diesen nichtterminalen X_i verzweigen die verbleibenden k - 1 inneren Knoten.

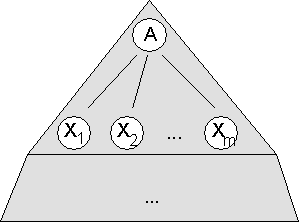
Abbildung 31 - Illustration eines A-Baum

Wenn X_i kein Blatt ist, dann ist X_i also Nichtterminalsymbol und Wurzel eines Unterbaums. Dieser X_i-Baum habe die Front a_i. Ist ein X_i allerdings Blatt und somit Nichtterminalsymbol, dann sei X_i = a_i. Für j < i sind ein X_j sowie etwaige Kinderknoten in Front des A-Baums weiter links von einem X_i mit seinen Kinderknoten. Dann setzt sich die Front a des A-Baums folgendermaßen zusammen

Die Grafik illustriert das mit der Darstellung von X_j- und X_i-Teilbäume nochmal

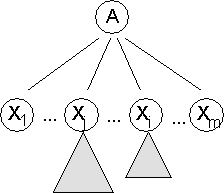
Abbildung 32 - A-Baum mit Kinderknoten und Xj-/Xi-Teilbäumen

Da A-Bäume k innere Knoten enthalten, ist die maximale Anzahl von inneren Knoten bei X_i‑Bäumen entsprechend k - 1. Ausnahme ist natürlich der Fall, dass ein X_i-Baum genau der A-Baum ist, was aber hier unbeachtet bleiben soll. Gemäß Induktionsannahme, dass der Satz in Hinrichtung für Bäume mit inneren Knoten k < 1 bereits bewiesen sei, folgt

Faßt man diese Teilableitungen für jedes X_i zusammen, ergibt sich für die Front des A‑Baums

Damit gilt . Wenn dies für alle Nichtterminalsymbole A gilt, dann auch für das Startsymbol S. Allerdings handelt es sich bei der durchgeführten Ableitung nur um eine mögliche Ableitung des Ableitungsbaumes.

Die Rückrichtung des Beweises erfolgt analog. Hier wird von einem gegebenen auf einen Ableitungsbaum geschlossen. Da sowohl Hin- als auch Rückrichtung in der Vorlesung ausgespart wurden, wird an dieser Stelle auf eine weitere Darlegung verzichtet, zumal die Ähnlichkeit von Rückrichtung und Hinrichtung sehr hoch ist. Stattdessen gehen wir lieber zum nächsten Thema.

14.1.5 Linksableitung

Werden in einer Ableitung die Produktionen immer zuerst auf die am weitesten links stehenden Nichtterminalsymbole angewandt, dann spricht man von einer Links- oder leftmost-Ableitung. Wendet man die Produktionen hingegen immer auf die rechte Seite an, so spricht man von Rechts- bzw. rightmost-Ableitungen.

Definition:

Für eine kontextfreie Grammatik ist eine Linksableitung (leftmost)

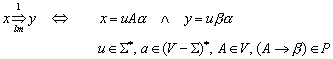
Die formale Definition sagt aus, dass in einem Ableitungsschritt (mit der Anwendung einer Produktion) immer das am weitesten links stehendene Terminalsymbol (das ist hier das A, gefolgt von einer belieben Kombination a aus Nichtterminal- und Terminalsymbolen) zuerst abgeleitet wird. Daraus folgen Ableitungen in n und beliebig vielen Schritten (transitive und reflexive Hülle).

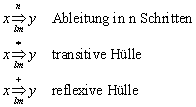
14.1.6 Eindeutigkeit

Wenn es eine Ableitung

gibt, dann existiert genau ein entsprechender Ableitungsbaum. Existiert umgekehrt ein Ableitungsbaum B mit der Front a (wie in den vorangegangenen Ausführungen mehrfach aufgetreten), dann gibt es im allgemeinen mehrere Ableitungen, die diesem Baum entsprechen. Allerdings gibt es nur genau eine Linksableitung für diesen Ableitungsbaum B.

Damit lassen sich Eindeutigkeit und Mehrdeutigkeit von Grammatiken definieren.

Definition:

Für eine kontextfreie Grammatik G gilt

und analog

Weiter ist eine kontextfreie Sprache L eindeutig, wenn es eine eindeutige kontextfreie Grammatik G gibt, für die L = L(G) gilt.

Umgekehrt heißt eine kontextfreie Sprache L inhärent mehrdeutig, wenn keine eindeutige kontextfreie Grammatik G mit L = L(G) existiert.

14.2 Vereinfachung kontextfreier Grammatiken

Grammatiken für kontextfreie Sprachen können überflüssige Produktionen und Nichtterminalsymbole enthalten. Mit verschiedenen Verfahren u. a. auch dem Umstellen auf Normalformen können Grammatiken auf einen einheitlichen und leichter zu untersuchenden Stand gebracht werden. In diesem Protokoll soll es um Entfernung von e-Produktionen gehen. Das sind Produktionen, bei denen auf der rechten Seite das leere Wort steht.

14.2.1 e-Produktionen

Solche Löschmöglichkeiten (auch Deletion genannt), sind für die Definition einer Sprache durch eine Grammatik nicht nötig. Eine Ausnahme muß gegeben sein, wenn die Sprache das leere Wort enthält. Dann kann das Startsymbol ins leere Wort übergehen. Enthält die Sprache das leere Wort nicht, so ist auch diese Produktion nicht nötig. Wir werden mit dieser Vorstellung zeigen, dass es zu beliebigen kontextfreien Sprachen L eine kontextfreie Grammatik gibt, die nur eine oder keine e-Produktionen enthält.

Definition:

Zu einer kontextfreien Sprache existiert eine kontextfreie Grammatik mit den Eigenschaften

Die Sprache L wird also von der Grammatik G erzeugt und verzichtet dabei auf e‑Produktionen. Lediglich der Übergang wird zugelassen, wenn das leere Wort Bestandteil von L ist.

Beweis:

Für jede kontextfreie Sprache L existiert eine kontextfreie Grammatik mit L = L(G’). Um auf die Sprache G zu gelangen, sind zwei Schritte zu gehen. Zunächst werden alle Nichtterminalsymbole aussortiert, die direkt oder über mehrere Produktionen zum leeren Wort e führen.

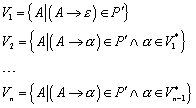
Damit werden schrittweise alle Nichtterminalsymbole in V_i übernommen, die direkt oder über andere V_j mit j < i zum leeren Wort führen. Da die Anzahl der Symbole in V’ nicht unendlich ist, sind nach N Läufen alle Nichtterminalsymbole gefunden, die direkt oder direkt aber nach maximal N Ableitungen zum leeren Wort kommen.

V_n sind dann die löschbaren Nichtterminalsymbole, d. h. Symbole, die mit endlich vielen Ableitungsschritten ins leere Wort e überführt werden können. Das wird in bekannter Notation festgehalten:

Daraus folgt

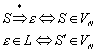
Nachdem die löschbaren Nichtterminalsymbole gefunden wurden, werden im zweiten Schritt die Produktionen auf Basis der verbliebenen Symbole umgebaut.

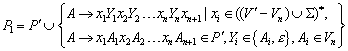
Daraus wird anschaulich klar, dass die Sprache L mit der so entworfenen Grammatik generiert werden kann und die Grammatik über die in der Definition vorgegebenen Eingenschaften verfügt.

15 Vorlesung vom 30. Mai 2000

15.1 Reduktion von Grammatiken

15.1.1 Definition Brauchbarkeit von Nichtterminalsymbolen

Sei eine kontextfreie Grammatik. Dann ist ein Nichtterminalsymbol definitionsgemäß dann nicht-überflüssig (brauchbar) wenn damit ein Wort generiert werden kann, und es vom Startsymbol aus erreichbar ist.

Formal bedeutet das:

und auch:

Die Umkehrung gilt dann natürlich auch. Ein Nichtterminalsymbol heißt dann überflüssig, wenn nicht (nicht-überflüssig ist). Also genau dann wenn die oben erwähnten zwei Bedingungen nicht zutreffen.

Satz:

Für jede kontextfreie Sprache (welche von einer kontextfreien Grammatik erzeugt wurde) gibt es eine kontextfreie Grammatik mit:

1. und

2. hat keine überflüssigen Symbole

Diese Grammatik kann man auch eine „reduzierte Grammatik“ nennen.

Beweis:

Sei nun die Sprache kontextfrei. Dann existierte eine kontextfreie Grammatik mit . Der Beweis erfolgt in zwei Schritten. Dabei ist zu beachten, dass es wichtig ist, die Reihenfolge der beiden Schritte genau einzuhalten. Aber dazu später:

· Schritt1: Man bilde die Menge indem man all die Nichtterminalsymbole auswählt, welche direkt ein Terminalsymbol generieren können. Rekursiv fährt man dann für fort all die Nichtterminalsymbole in die Menge aufzunehmen, die Nichtterminalsymbole enthalten, die Terminalsymbole erzeugen. Da die Zeichenmenge endlich ist muss es ein geben, für das die zwei so entstandenen Mengen gleich sind. Alle weiteren Mengen sind dann auch gleich. Formal ausgedrückt bedeutet dies:

Nun betrachtet man alle Symbole in . Man sieht, dass sie alle Terminalsymbole generieren. Die Umkehrung gilt auch, wird ein Terminalsymbol generiert, so ist das dafür verantwortliche Nichtterminalsymbol in . Die Sprache ist genau dann leer, wenn dass Startsymbol nicht in ist. Man definiert nun die Grammatik . Hierbei ist beschränkt auf Nichtterminalsymbole, welche in Terminalsymbole überführt werden können und ist die Menge der Produktionen, welche Terminalsymbole produzieren.

Formal:

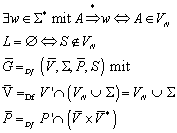
Somit haben wir nun nur noch Nichtterminalsymbole, welche in Terminalsymbole überführt werden können.

· Schritt 2: Nun gilt zu überprüfen welche Symbole eigentlich erreichbar sind. Dazu betrachtet man alle Nichtterminalsymbole , welche auf der Rechten Seite einer Produktion auftauchen. Man definiert rekursiv die Übernahme aller Nichtterminalsymbole , welche über ein weiteres Nichtterminalsymbol erreichbar sind, das wiederum vom Startsymbol erreichbar ist. Auf diese Weise bekommt man alle Symbole, welche in Terminalsymbole überführt werden können und die vom Startzustand aus erreichbar sind. Ist dann einmal Gleichheit von zwei aufainander folgenden Mengen und erreicht, so bleibt diese Gleichheit bestehen. Dieser Fall muss auftreten, da der Symbolvorrat endlich ist.

Formal drückt man das so aus:

Ein Nichtterminalsymbol ist also dann enthalten, wenn es erreichbar ist. Wieder gilt auch die Umkehrung. Ist ein Element erreichbar, so ist es auch in der Menge enthalten. Schließlich ist um all die Nichtterminalsymbole reduziert, die nicht erreichbar sind. Ebenso werden die Produktionen aus genommen, welche nicht verwendet werden können.

Formal:

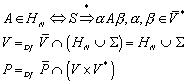
15.1.2 Das Problem der Ausführung der beiden Schritte

Kann nun Schritt 2 das Ergebnis von Schritt 1 kaputtmachen? Angenommen es gäbe kein Wort , welches von erzeugt wird. Dann muss aufgrund von Schritt 1 ein Symbol existieren, das Abgeleitet werden könnte, jedoch aufgrund von Schritt 2 entfernt worden ist. Die Produktion war also nicht erreichbar. Formal:

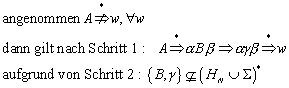
Da aber erreichbar ist, ist auch B und alle Nichtterminalsymbole in erreichbar.

Die Antwort darauf ist also Nein, jedoch ergibt sich ein Problem wenn man Schritt 2 vor Schritt 1 ausführt. Dies wird durch das folgende Beispiel deutlich:

Beispiel:

Für nebenstehende Grammatik ergibt sich durch den ersten Schritt zunächst:

Hier wurden also die Nichtterminalsymbole genommen, die direkt in Terminalsymbolen enden.

Nun wurde das Startsymbol aufgrund der Produktion übernommen.

Die weitere Betrachtung zeigt, dass keine weiteren Nichtterminalsymbole übernommen werden müssen also folgt:

Mit wie nebenstehend definiert, kann man die Grammatik aufstellen.

Für den zweiten Schritt ergibt sich dann:

Dabei wurde jeweils nach der Erreichbarkeit der Symbole gesehen. Zuerst wird das Startsymbol eingeschlossen, das einzige von dort aus zu erreichende Symbol ist dann gewesen.

Was passiert nun, wenn man diese Reihenfolge vertauscht?

Durch die Anwendung des zweiten Schrittes zuerst ergibt sich:

Dabei wurde jeweils nach der Erreichbarkeit der Symbole gesehen. Zuerst wird das Startsymbol eingeschlossen, dann übernimmt man die Symbole und schließlich noch .

Wendet man nun den ersten Schritt an, so übernimmt man zuerst und kommt zu:

nun nimmt man noch das Startsymbol hinzu, da gilt :

Für alle folgenden Iterationen gilt:

Man bekommt also ein anderes Ergebnis. Die überflüssigen (nicht erreichbaren) Produktionen und wurden mit übernommen. Der Grund dafür liegt hier bei der Produktion hier kann nicht in ein Terminalsymbol überführt werden. hingegen kann in ein Terminalsymbol überführt werden. Es ist also wichtig die Reihenfolge einzuhalten.

Wie kann man die Grammatik nun noch weiter minimieren?

15.1.3 Zyklische Produktionen

Sei nun eine Grammatik. Dann heißt eine zyklische Produktion. Da wir eine kontextfreie Grammatik gegeben haben, kann man zyklische Produktionen herausschneiden. Die Ableitungsschritte der zyklischen Produktionen müssen dann jedoch simuliert werden.

Satz:

Sei eine kontextfreie Sprache. Dann gibt es eine kontextfreie Grammatik G mit:

Beweis:

Sei eine kontextfreie Grammatik mit . Dann gilt für alle :

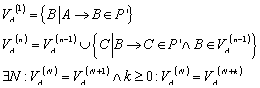
Als neue Produktionen gelten also die „alten“ Produktionsregeln, ohne zyklische Produktionen, jedoch erweitert um die Produktionen, die durch den Zyklus erreicht werden könnten.

Offensichtlich ist nun .

Beispiel:

15.1.4 Zusammenfassung

Eine kontextfreie Grammatik heißt reduziert, genau dann wenn:

1. hat keine Produktionen vom Typ mit . Es gibt also keine zyklischen Produktionen.

2. Es gibt keine -Produktionen. Das Startsymbol kann nur dann gleich sein, wenn es in der Sprache ist.

· taucht auf keiner rechten Seite auf,

· Alle Symbole können keine Produktionen haben.

3. Jedes Nichtterminalsymbol ist brauchbar. hat keine überflüssigen Symbole und Produktionen d.h.:

Satz:

Sei kontextfrei. Dann existiert eine reduzierte kontextfreie Grammatik mit .

Beweis:

Sei kontextfrei. Dann existiert eine kontextfreie Grammatik mit :

a) Man modifiziere , um Eigenschaft 2) zu erhalten, und erhält ,

b) Man modifiziere zu mit Eigenschaft 1)

c) Man modifiziert schließlich zu mit Eigenschaft 3)

ist dann reduziert und es gilt weiterhin .

Bemerkung:

Es ist jedoch darauf zu achten die Reihenfolge zu beachten. Wie wir schon an dem Beispiel gesehen haben, kann die Ausführung in anderer Reihenfolge das Ergebnis verändern. Insbesondere bedeutet das für den letzten Beweis:

a) man muss A) vor B) ausführen, da A) Produktionen vom Typ mit einführen kann.

b) B) zerstört nicht die Eigenschaft 2)

c) C) zerstört nicht die Eigenschaften 1) und 2)

16 Vorlesung vom 6. Juni 2000

16.1 Chomsky-Normalform

Satz (Chomsky-Normalform):

Sei eine reduzierte kontextfreie Grammatik. Dann existiert eine reduzierte kontextfreie Grammatik mit

2. P‘ enthält nur Produktionen vom Typ

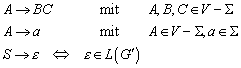
Diese reduzierte Form, die nur noch einen binären Ableitungsbaum erlaubt, heißt auch „Chomsky-Normalform“.

Beweis

Sei reduziert. Man konstruiert G‘ in mehreren Schritten. Ziel ist es, alle Produktionen, die auf der rechten Seite mehr als zwei Nichtterminale oder mehr als ein Terminal bzw. das leere Wort stehen haben, umzubauen. Hierzu bauen wir neue Produktionsregeln aus den alten (P) auf:

diese Menge nimmt also alle diejenigen Regeln aus P auf, die gemäß unserer Bedingung 2) ohnehin in P‘ enthalten sein dürften. Wir definieren nun einen Homomorphismus h(), einerseits die Terminale auf neue Nichtterminale (in eckigen Klammern geschrieben) abbildet und andererseits die Nichtterminale ohne Änderung überträgt:

Damit bauen wir eine neue Produktionsmenge auf, die alle Produktionen aufnimmt, die in P auf der rechten Seite mehr als zwei symbole (Terminale bzw. Nichtterminale) enthielten. Damit haben wir sämtliche Regeln aus P abgehandelt.

Wir müssen jetzt P₁ und P₂ noch zusammenfassen und die neuen Nichtterminale in eckigen Klammern zurück auf die ursprünglichen Terminale abbilden:

Wir erhalten nun also offensichtlich mit . Dabei gilt:

Nun haben wir in P₂ noch Regeln enthalten, die mehrere Nichtterminale auf der rechten Seite stehen haben. Diese reduzieren wir nun durch Aufblähen unserer Produktionsregelmenge, indem wir jede Regel in mehrere aufsplitten. Dies wird durch das spätere Beispiel noch deutlicher.

Wir ersetzen also jede Produktion aus P₃ mit der Form durch

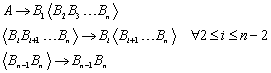
Dabei sind die neue Nichtterminale, die V‘ hinzuzufügen sind. Somit erhält man mit .

Satz:

Sei eine kontextfreie Grammatik in Chomsky-Normalform. Dann gilt:

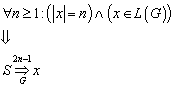
Die Anzahl der Schritte (2n-1) läßt sich aus dem folgenden Schaubild ersehen:

Abbildung 33

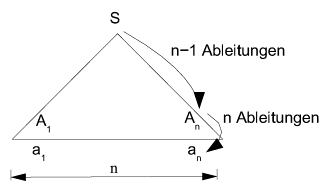
Beispiel

Wir wollen die Grammatik mit auf Chomsky-Normalform bringen und wenden hierzu die aus dem obigen Satz bekannten zwei Schritte an:

P	Schritt 1	Schritt 2

Damit haben wir eine Grammatik in Chomsky-Normalform mit den in Schritt 2 bezeichneten Produktionen und den Nichtterminalen:

17 Pushdown-Automaten

17.1 Einführung

Wir kommen nun zu dem Thema der „Pushdown-Automaten“ („Kellerautomaten“). Wie wir später sehen werden, beschreiben kontextfreie Grammatiken und Pushdown-Automaten (PDA) dieselben Sprachen.

Im Wesentlichen ist ein PDA ein endlicher Automat, der sowohl über ein Band als auch über einen Stack (Keller) gesteuert wird. Weiter besitzt er eine endliche Kontrolle. Der Stack ist eine Symbolfolge über einem Alphabet. Wir stellen uns den Keller um 90° gekippt vor, so daß das erste Kellersymbol („Top“) immer das am weitesten links stehende Symbol ist.

Der Automat kann auf zwei Arten arbeiten: Entweder liest er ein Symbol der Eingabe und kann in Abhängigkeit des aktuellen Zustandes und des obersten Elementes des Stacks den zustand wechseln. Das oberste Element des Stacks wird dann entfernt und eventuell durch ein neues Alphabetsymbol, einer Symbolfolge oder durch das leere Wort ersetzt. Sodann geht der Lesekopf eine Position auf dem Band nach rechts.

In der zweiten Arbeitsweise liest der Automat kein Symbol (eine sogenannte „“) vom Eingabeband (der Lesekopf bewegt sich also nicht). Genau wie oben können Zustand und/oder Stack verändert werden.

Bildlich kann man sich das ganze wie in Abbildung 34 vorstellen:

Abbildung 34

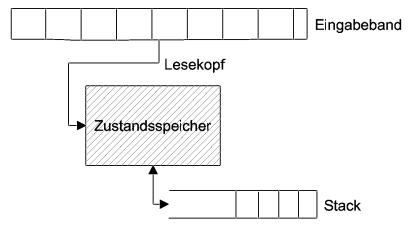
17.2 Formale Definition, Konfiguration, Akzeptierung

Definition (Pushdown-Automat)

Ein Pushdown-Automat (PDA, Kellerautomat) ist ein 7-Tupel mit:

1. Q ist eine endliche Menge von Zuständen

2. ist eine endliche Menge von Eingabesymbolen

3. ist eine endliche Menge von Kellersymbolen

4. ist der Anfangszustand

5. ist das Anfangskellersymbol (also das Symbol, mit dem der Keller initialisiert wird)

6. ist die Menge der akzeptierenden Zustände

In Punkt 7 ist die Bedingung „A endlich“ eingefügt, da unendlich sein könnte (wegen der Kleeneschen Hülle).

Wir können zwei Feststellungen machen:

1. Ein PDA ist in der Regel nicht deterministisch. Dies ergibt sich aus der Tatsache, daß eine Funktion ist, die auf eine Menge abbildet.

2. Die Stillstandsbewegung des „Lesekopfs“ ergibt sich aus der Funktionsverwendung . Dies bedeutet, dass das Eingabesymbol nicht gelesen wird und nur eine Zustandsveränderung und/oder Stackveränderung vorgenommen wird.

Definition (Konfiguration)

Sei ein PDA. Dann ist eine Konfiguration von M. Die Bedeutung einer solchen Konfiguration ist:

· augenblicklicher Zustand

· noch verbleibende Eingabe mit a als nächstem Symbol,

· Kellerinhalt, mit A als oberstem Symbol,

Anmerkung: Eine Konfiguration kann man also als den Gesamtzustand eines PDAs ansehen. Sie beschreibt zu jedem Zeitpunkt genau den Zustand eines PDAs.

Definition

Sei ein PDA. Dann definieren wir die folgenden Operationen:

Seien c und c‘ zwei beliebige Konfigurationen. Dann gilt:

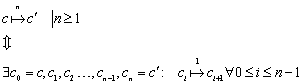
Für alle Konfigurationen c gilt:

Diese Definition bezieht sich also auf die Übergänge innerhalb des Automaten, die durch die Funktion realisiert werden und gibt uns eine einfachere Notation.

Die folgende Definition zeigt uns, dass wir drei Möglichkeiten haben, wie wir die Akzeptierung eines Wortes definieren. Es ist daher immer wichtig, zu wissen, von welcher Akzeptierungsart gesprochen wird.

Definition (Akzeptierungsarten)

Sei ein PDA. Dann existieren drei Möglichkeiten der Akzeptierung:

1. Akzeptierung durch akzeptierende Zustände und leeren Stack:

2. Akzeptierung nur durch akzeptierende Zustände:

3. Akzeptierung nur durch leeren Stack:

Beispiel eines PDA

Abbildung 35

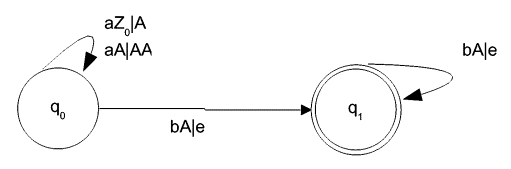
Dieser PDA stellt die Sprache dar. Dabei bedeutet , dass bei Lesen des Zeichens a und wenn Z₀ das oberste Element des Stacks ist, Z₀ vom Stack entfernt wird und durch A ersetzt wird.

Würde man die Akzeptierung vom Typ 2) annehmen, so gälte , da bei dieser Variante bereits akzeptiert wird, wenn nur ein akzeptierender Zustand vorliegt.

In diesem Beispiel realisiert der Stack also eine Art Zähler.

17.3 Äquivalenz von PDA und kontextfreier Grammatik

Satz (Äquivalenz Akzeptierungsarten):

Sei eine Sprache. Dann sind die folgenden Aussagen gleichwertig:

1. für einen PDA M₁

2. für einen PDA M₂

3. für einen PDA M₃

Beweis

1)Þ2):

Sei für . Wir definieren einen zweiten PDA:

mit . Die Übergangsfunktion definieren wir so:

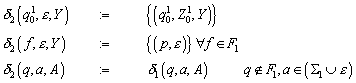
Man kann verifizieren, dass gilt:

und damit .

Bildlich kann man sich die Konstruktion so vorstellen, dass zu Anfang ein „Stoppersymbol“ Y auf den Stack gelegt wird, dann der alte Automat M₁ normal laufen gelassen wird. Wenn dieser ein Wort akzeptiert, dann ist der Stack normalerweise leer. In unserem Falle wird also noch Y auf dem Stack liegen. Wenn das der Fall ist, dann wird in den Zustand p verzweigt, der der einzige akzeptierende Zustand ist. Aufgrund dieses Zustandes akzeptiert nun der Automat M₂ aufgrund von alleinig wegen des Zustandes.

2)Þ3):

Sei für . Wir definieren einen neuen PDA M₃ wie folgt:

mit . Wir haben dann und definieren die Übergangsfunktion so:

Bei der zweiten Zeile von zeigt sich der Nichtdeterminismus. Hier steht für den Start des Löschens des Stacks und für das Weiterarbeiten in der alten Maschine.

Die Funktionsweise ist die folgende: Solange wir in einem Zustand aus dem alten Automaten M₂ sind, arbeiten wir im alten Automaten (letzte Regel). Sind wir in einem akzeptierenden Zustand des alten Automaten, so löschen wir den Stack (zweite Regel erster Teil bzw. dritte Regel) oder arbeiten im alten Automaten weiter (zweite Regel zweiter Teil), da man auch in einem akzeptierenden Zustand im alten Automaten weiterarbeiten könnte ohne direkt abzubrechen.

Dies alles zeigt uns (was man auch formal beweisen könnte), dass gilt

und damit .

3)Þ1):

Sei für . Dann definieren wir einfach einen Automaten, der die gesamte Zustandsmenge akzeptiert:

Damit gilt offensichtlich , da der Automat M₁ mit der Definition von T nur dann ein Wort akzeptiert, wenn der Zustand akzeptiert wird und der Stack leer ist. Da M₃ aber nur dann akzeptiert, wenn der Stack leer ist und in M₁ alle Zustände akzeptieren, gilt dies bereits.

17.3.1 Äquivalenz PDA und kontextfreie Grammatiken

Satz (Äquivalenz PDA/ kontextfreie Grammatik):

Sei eine kontextfreie Grammatik in Chomsky-Normalform. Dann existiert ein PDA M, so dass .

Beweis:

Wir definieren zunächst einen PDA und zeigen dann, dass das Gesagte gilt. Sei also

der PDA. Wir betrachten nun die Definition von . Hieraus folgt die Definition der Übergangsfunktion:

Mit der ersten Regel können wir das jeweils oberste (linkeste) Stacksymbol durch Produktionen ersetzen und damit den Stack „aufblähen“ (nichtdeterministisch, wie man natürlich an der Mengenklammer sieht). Dabei handelt es sich um reine -Bewegungen, d.h. es wird kein Zeichen der Eingabe gelesen, sondern es werden lediglich sämtliche möglichen Produktionen des obersten Stacksymbols, das ein Nichtterminal ist, „durchprobiert“.

Die zweite Regel dient dazu, Terminale wieder vom Stack löschen zu können. Diese Löschen kann man sich wie ein „Matching“ vorstellen, d.h. ein Terminal wurde als „möglich“ erkannt und vom Stack gelöscht. Dabei wird der Lesekopf auf das nächste Eingabesymbol weitergeschoben.

Wir vollziehen den Beweis nun in zwei Schritten. Die beiden Schritte zusammen ergeben den Gesamtbeweis:

1. und 2. zusammen ergeben die Aussage, wie wohl offensichtlich ist (1 ist die eine Richtung und 2 die andere).

Beweis von 1:

Wir beweisen per Induktion:

Induktionsverankerung (n=1):

Es sei . Dann folgt daraus und (also dass w ein einzelnes Eingabesymbol ist). Hieraus folgt mit der Definition von (Punkt 1)(siehe ): . Daraus wiederum folgt:

(der letzte Ableitungsschritt gilt wegen Punkt 2 der Definition von (siehe ).

Induktionsannahme n:

Für alle gelte die folgende Implikation:

Induktionsschritt ():

Wir haben . Dies ist äquivalent zu . Die Einzelableitung gilt, weil wir angenommen haben, dass die kontextfreie Grammatik G in Chomsky-Normalform vorliegt. Mit Regel 1 der Definition von (siehe ) folgt:

also . Es gilt weiter mit und mit . Damit gilt nach zweimaliger Anwendung der Induktionsannahme

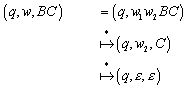
Damit gilt insgesamt

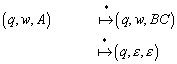
und damit die Behauptung.

18 Vorlesung vom 8. Juni 2000

18.1 Für jede CFL existiert ein PDA

18.1.1 Fortsetzung des Beweises vom 06. Juni 2000

Der Beweis zur Äquivalenz von PDA und kontextfreier Grammatik wurde in der Vorlesung vom 06. Juni 2000 begonnen, und wird hier fortgeführt.

Es ist zu zeigen:

1: „Hin-Richtung“:

2: „Rückrichtung“:

Das Symbol „A“ sei hierbei ein Nichtterminal der kontextfreien Grammatik.

Die „Hin-Richtung“ wurde bereits gezeigt. Nun folgt der Beweis der „Rückrichtung“, d.h. wir müssen zeigen, dass jedes Wort, welches unser Automat akzeptiert, auch durch die Grammatik erzeugt werden kann. Diesen Beweis erbringen wir durch vollständige Induktion über die Länge der Produktion n.

Wir erinnern uns: Der PDA wurde so konstruiert, dass die Terminalsymbole der kontextfreien Grammatik als Bandalphabet dienen, und sowohl die Terminalsymbole als auch die Nichtterminalsymbole der kontextfreien Grammatik als Stacksymbole dienen.

Induktionsverankerung (n=1):

Für n=1 gilt:

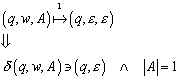
Bei der Definition unseres Kellerautomaten, dem ja eine kontextfreie Grammatik zugrunde liegt, haben wir einen Zustandsübergang genau dann hinzu genommen, wenn für diese kontextfreie Grammatik mindestens eine von zwei Bedingungen erfüllt ist:

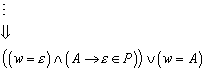
Das bedeutet in geschriebener Sprache, dass entweder a) kein Symbol vom Band gelesen wird, und ein auf dem Stack liegendes „Nichtterminal“[13] durch das „Terminal“ „leeres Wort“ ersetzt wird, oder b) das vom Band gelesene „Terminal“ dem (einzigen) Zeichen auf dem Stack entspricht, und der Stack daher leergeräumt wird.

Fall a) tritt definitionsgemäß (siehe Definition unseres PDA) genau dann ein, wenn in der kontextfreien Grammatik ein Übergang des Nichtterminales in das Terminal „leeres Wort“ existiert. Da die kontextfreie Grammatik in Chromsky-Normalform ist, kann es sich nur um den Übergang des Startsymboles S in das leere Wort handeln. Unser Nichtterminalsymbol A muss dann also („von vorne herein“) das Startsymbol S gewesen sein, und es muss eine Produktionsregel geben, die das Startsymbol S in das leere Wort übergehen lässt.

In diesem Fall handelt es sich um einen e-Übergang:

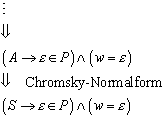
Da es also diese Produktionsregel gibt, gilt:

Damit ist für die Produktionslänge n=1 und den Fall a) gezeigt, dass jedes Wort, dass unser PDA akzeptiert, von der kontextfreien Grammatik erzeugt wird.

Fall b) ist noch einfacher. Fall b) kann nämlich gar nicht eintreten, da das Symbol auf dem Stack (A) ein „Nichtterminalsymbol“ ist. Demzufolge wird es auf dem Band nie das Zeichen A geben, und Fall b) tritt nie ein. Damit ist für die Produktionslänge n=1 (für Fall a) und Fall b)) gezeigt, dass jedes Wort, dass unser PDA akzeptiert, von der kontextfreien Grammatik erzeugt wird.

Induktionsannahme:

Induktionsschritt ():

Wir betrachten nun ausdrücklich nur Ableitungen, die eine Länge größer als zwei haben. Dies geschieht aber in Übereinstimmung mit dem Skript zur Vorlesung[14]. Der Fall, dass das „Nichtterminal“ A, das auf dem Stack liegt, im ersten Zustandsübergang durch ein Terminal ersetzt wird, kann nicht eintreten. Könnte er eintreten, wäre der Stack nach dem zweiten Zustandsübergang bereits leer – und damit die Verarbeitung des PDA beendet; das ist aber ein Widerspruch zu der Annahme, dass mindestens drei Zustandsübergänge erfolgen.

Daher gilt:

Dieser Übergang des Stacksymboles A in die Stacksymbole B und C kann nur definiert worden sein, wenn die kontextfreie Grammatik die entsprechende Produktion enthält:

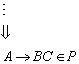
Der Ausdruck bedeutet nichts anderes, als dass das vorhandene „Nichtterminal“ auf dem Stack durch zwei andere „Nichtterminale“ ersetzt wird. Je nach Länge des Eingabewortes geschieht dies einige Male. Letzten Endes werden aber alle so auf dem Stack abgelegten „Nichtterminale“ wieder „abgebaut“, das bedeutet Stück für Stück durch Vergleichen mit dem Eingabewort durch das leere Wort ersetzt – bis der Stack irgendwann leer ist. Insbesondere bedeutet das, dass „C“ nicht vom Stack gelöscht werden kann, bevor nicht auch „B“ vom Stack gelöscht wurde. Und wenn wir einen Schritt weiter denken, und davon ausgehen, dass sowohl C als auch B auf dem Stack durch mehrere andere „Nichtterminale“ ersetzt werden, bedeutet das trotzdem, dass die „Nichtterminale“, die aus B hervorgegangen sind, nicht gelöscht werden können, bevor nicht die „Nichtterminale“ gelöscht wurden, die aus C hervorgegangen sind.

Daher lässt sich die Verarbeitung des Eingabewortes w wie folgt zerlegen:

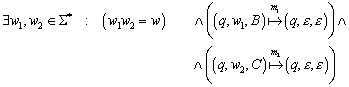
mit und . Unter Zuhilfenahme der Induktionsannahme folgt daraus:

Den Übergang von A nach BC haben wir selber in definiert, daher gilt:

Damit ist der Induktionsbeweis abgeschlossen:

Gesamtbeweis:

Wenn wir nun in den (bewiesenen) Behauptungen und das allgemeine „Nichtterminal“ A durch das spezielle Nichtterminal, das Startsymbol S ersetzen, erhalten wir:

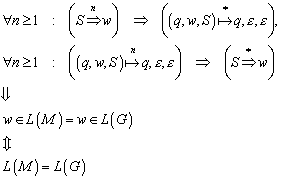
19 Vorlesung vom 15. Juni 2000

19.1 Greibach Normalform (GNF)

19.1.1 Vorbemerkung

Neben der Chomsky Normalform ist auch die Greibach Normalform als weitere standardisierte Darstellungsform für kontextfreie Grammatiken bekannt. Hier sind alle Produktionen derart gestaltet, dass die rechte Seite immer mit einem Terminalsymbol beginnt und keines oder beliebig viele Nichtterminalsymbolen folgen.

Um zu zeigen, dass sich jede kontextfreie Grammatik für Sprachen ohne leeres Wort e in Greibach Normalform bringen lässt, wie wir in den folgenden Abschnitten zeigen werden, muss es möglich sein, äquivalente Grammatiken aufzustellen, bei denen mehrere Ableitungsschritte in einzelnen Produktionen zusammengefasst werden. Dass solche Zusammenfassungen möglich sind, wird im Folgenden gezeigt.

Eine A-Produktion ist eine Produktion der Form

mit einem Nichtterminalsymbol A auf der linken Seite. Bei einer kontextfreien Grammatik gebe es eine A-Produktion mit B-Produktionen

Dann gibt es eine aus G hervorgehende kontextfreie Grammatik mit neuen Produktionen

die durch Ableiten von aus G mit entstehen. Die Produktion ist dann überflüssig und fehlt in G₁. Dann gilt .

Beweis:

Der Beweis ist einfach, da sich ergibt, wenn man für jede Ableitung

in G₁ das entsprechende

verwendet. Umgekehrt ist , da die einzige Produktion ist, die in G und nicht in G₁ enthalten ist. Immer, wenn benötigt wird, folgt in einem späteren Ableitungsschritt , was man in G1 in einem einzigen Ableitungsschritt mit realisiert wird. Folglich ist .

19.1.2 Umwandlung von linksrekursiven in rechtsrekursive Produktionen

Mit der im vorangegangen Abschnitt vorgestellten Möglichkeit, Zusammenfassungen von Ableitungen vorzunehmen, kann man bereits viele Produktionen in Greibach Normalform überführen. Problematisch wird es allerdings bei linksrekursiven Produktionen, die Nichtterminalsymbole auf sich selbst und weitere Symbole abbilden, da diese nicht ohne Weiteres in die gewünschte Form zu bringen sind.

Solche Produktionen der Gestalt

heißen linksrekursiv. Um sie kompatibel für die Greibach Normalform zu machen, kann man äquivalente rechtsrekursive Produktionen einführen. Gegeben sei eine Menge von A-Produktionen

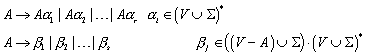
wobei die oberen Produktionen linksrekursiv und die unteren nicht linkrekursiv sind. Damit können die Wörter abgeleitet werden, die durch den regulären Ausdruck

beschrieben werden. Dabei handelt es sich um Wörter, die aus einem b_j an erster Stelle und beliebig vielen folgenden a_i bestehen. Diese Wörter lassen sich genauso durch Hinzufügen eines neuen Nichtterminalsymbols B mit Produktionen der folgenden Form erzeugen

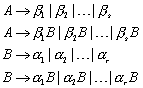
Damit liegen dann keine linksrekursiven, sondern rechtsrekursive Abbildungen vor, die die gleichen Wörter generieren und die zugehörigen Grammatiken somit die gleiche Sprache beschreiben.

Formaler gesprochen, gibt es zu einer kontextfreien Grammatik mit linksrekursiven Produktionen eine entsprechende Grammatik mit rechtsrekursiven Produktionen. Dabei sind alle Produktionen identisch, außer den linksrekursiven, die durch rechtsrekursive ersetzt werden.

G habe nun Produktionen der Form

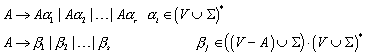
und G₁ entsprechend zusätzliche

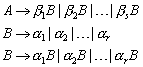
wobei die in G₁ nicht mehr auftauchen. Dann gilt .

Die folgende Illustration verdeutlicht die Ableitungsschritte.

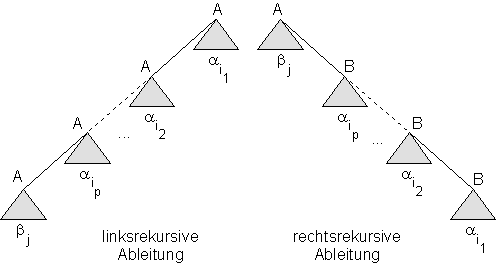
Abbildung 36 - Links- und rechtrekursive Ableitungen

Beweis:

In G endet jede Ableitung von mit . Damit erhält man

was in G₁ folgendermaßen erzielt wird

Da beide Ableitungen zu den gleichen Wörtern führen, die dem oben genannten regulären Ausdruck entsprechen, gilt . Somit wurde gezeigt, dass sich linksrekursiven Produktionen unter Zuhilfenahme neuer Nichtterminalsymbols B_k sowie weiterer Produktionen in rechtsrekursive umwandeln lassen und dabei die mit der Grammatik erzeugte Sprache erhalten bleibt.

19.1.3 Kontextfreie Grammatiken in Greibach Normalform (GNF)

Satz:

Jede kontextfreie Sprache L ohne leeres Wort e kann durch eine kontextfreie Grammatik G generiert werden, deren Produktionen die Form

haben. A und B_i sind Nichtterminalsymbole, a ist ein Terminalsymbol. Sind alle Produktionen von dieser Form, heißt die Grammatik in Greibach Normalform.

Beweis:

Der Nachweis über die Richtigkeit dieser Aussage wird mit Hilfe eines Algorithmus erbracht, der eine beliebige Grammatik , die sich bereits in Chomsky Normalform (CNF) befindet, in eine Grammatik in Greibach Normalform (GNF) umwandelt.

Der Umwandlungsprozess wird in drei Schritten vorgenommen. Zunächst nummerieren wir die Nichtterminalsymbole der Ausgangsgrammatik G₁ mit i = 1...m

mit dem Ziel, alle Produktionen in die Form

zu überführen. Dazu durchlaufen wir alle A_i-Produktionen mit und i = 1...m und ersetzen jeweils - wie in der Vorbemerkung gezeigt - die A_j mit allen A_j-Produktionen. Für den Fall, dass eine linksrekursive Produktion auftritt, werden wie im vorherigen Abschnitt beschrieben, ein neues Nichtterminalsymbol und neue Produktionen eingeführt und die linksrekursive in eine rechtsrekursive Produktion umgewandelt.

Am Ende dieses ersten Schrittes haben wir Produktionen erhalten, für die mit i < j gilt. Die Produktionen für A_m sind dann in Greibach Normalform . Algorithmisch betrachtet sieht die Sortierung nach i < j so aus

for i := 1 to m do
for j := 1 to i - 1 do

foreach A_i -> A_jaÎ P₁ do

Füge hinzu A_i -> b₁a|b₂a|...|b_safür alle
Produktionen A_j -> b₁a|b₂a|...|b_sa ;

Entferne A_i -> A_ja ;

next
next j

if A_i -> A_iaÎ P₁ then

Füge Nichtterminalsymbol B_i hinzu ;

Füge hinzu A_i -> b₁B_i|b₂B_i|...|b_sB_i für alle

Produktionen A_j -> b₁|b₂|...|b_s mit A_i nicht erstem Zeichen von ß_l ;

Füge hinzu B_i -> a₁|a₂|...|a_r ;

Füge hinzu B_i -> a₁B_i|a₂B_i|...|a_rB_i ;

Entferne A_i -> A_ia ;

endif

next i

Im zweiten Schritt können wir die so geordneten Produktionen in Greibach Normalform überführen, indem wir sukzessive alle A_i-Produktionen beginnend bei A_m (das ja bereits ein Terminalsymbol als erstes Zeichen auf der rechten Seite und dann wegen der ursprünglichen Chomsky Normalform von G1 folgende Nichtterminalsymbole hat, also in Greibach Normalform ist) in die rechte Seite der A_i-1-Produktion einsetzen. Da i < j für alle Produktionen gilt, sind so im Anschluss an diesen Schritt alle Produktionen in Greibach Normalform. Algorithmisch kann das folgendermaßen beschrieben werden

for i := m - 1 downto 1 do
foreach A_i -> A_jaÎ P₁ mit i < j do

Füge hinzu A_i -> b₁a|b₂a|...|b_sa für alle
Produktionen A_j -> b₁a|b₂a|...|b_sa ;

Entferne A_i -> A_ja ;

next
next I

Im Anschluss daran befinden sich alle A_i-Produktionen in Greibach Normalform. Bleiben nur noch die möglicherweise hinzugekommenen B_i-Produktionen, deren rechte Seite im dritten und letzten Schritt analog umgeformt werden.

Da die ursprüngliche Grammatik G₁ in Chomsky Normalform ist, besteht die rechte Seite jeder Produktion entweder aus einem Terminalsymbol oder aus zwei Nichtterminalsymbolen. Durch die in den beiden ersten Schritten vorgenommen Umformungen sind deswegen keine Terminalsymbole weiter nach rechts gewandert, sondern können nach wie vor nur an erster Stelle stehen, wie es die Greibach Normalform fordert.

Bei den B_i-Produktionen besteht die rechten Seite ausschließlich aus Nichtterminalsymbolen. Da nach dem zweiten Schritt alle A_i-Produktionen in Greibach Normalform sind, muss im dritten Schritt lediglich das erste Nichtterminalsymbol der rechten Seite einer B_i-Produktion durch die rechte Seite der jeweiligen A_i-Produktion ersetzt werden (siehe Vorbemerkung) und folglich sind dann auch die B_i-Produktionen in der gewünschten Greibach Normalform.

19.1.4 Beispiel 1

Gegeben sei eine Grammatik mit den zugehörigen Produktionen

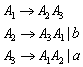
Diese wird im Folgenden in Greibach Normalform überführt.

1. Schritt

Das Umwandlungsverfahren in Greibach Normalform beruht auf Ausgangsgrammatiken in Chomsky Normalform. Die hier gegebene Grammatik liegt in CNF vor, da auf der rechten Seite entweder zwei Nichtterminalsymbole oder ein Terminalsymbol stehen. Wir können daher direkt mit der Umwandlung in GNF beginnen.

Die Produktionen müssen alle in die Form mit i < j gebracht und mögliche linksrekursive Produktionen in rechtsrekursive umgewandelt werden. Für die A₁- und A₂-Produktionen ist die Bedingung bereits gegeben, in die A₃-Produktion wird die rechte Seite von A₁ eingesetzt.

Dann erhält man

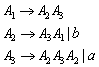
und in einem weiteren Schritt wird A₂ in der rechten Seite von A₃ durch A₃A₁ und b ersetzt, so das man folgende Menge von Produktionen erhält

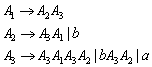
Die A₃-Produktion entpuppt sich jetzt als eine linksrekursive Produktion, die durch Hinzufügen eines Nichtterminalsymbols B₃ und weiterer Produktionen entfernt wird.

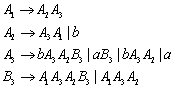
2. Schritt

Da sich jetzt alle Produktionen der Bedingung mit i < j genügen und A_m = A₃ bereits in Greibach Normalform ist, können wir die anderen A_i-Produktionen auch beginnend bei A_m‑1 = A₂ in die gewünschte Form umgestalten.

Für A₂ erhalten wir dann

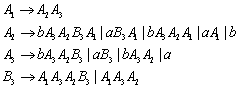
und entsprechend für A₁

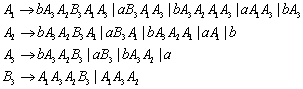
Damit sind alle A_i-Produktionen in Greibach Normalform. Fehlen noch die B_i-Produktionen.

3. Schritt

In das Nichtterminalsymbol der rechten Seite der beiden B₃-Produktionen werden alle fünf A₁-Produktionen eingesetzt, so dass 10 neue Produktionen entstehen.

Somit erfüllen alle Produktionen die Bedingung der Greibach Normalform, dass die rechte Seite immer aus einem Terminalsymbol gefolgt von keinem oder beliebig vielen Nichtterminalsymbolen besteht. Zu bemerken ist, dass aus den 5 Produktionen der Grammatik in Chomsky Normalform immerhin 24 Produktionen sowie ein weiteres Nichtterminalsymbol in Greibach Normalform geworden sind.

19.1.5 Beispiel 2

Gegeben sei eine Grammatik mit den zugehörigen Produktionen

1. Schritt

Das Umwandlungsverfahren in Greibach Normalform beruht auf Ausgangsgrammatiken in Chomsky Normalform. Die hier gegebene Grammatik liegt in CNF vor, wir können daher direkt beginnen.

Zunächst werden die Nichtterminalsymbole durchnummeriert. Sagen wir, S sei das erste und A das zweite Nichtterminalsymbol, also A₁ = S und A₂ = A, wobei wir aufgrund der Einfachheit auf diese Umbenennung verzichten können und die Reihenfolge im Hintergrund behalten. Dann ist die Zuordnung S ® AA in Ordnung, A ® SS muss jedoch umgewandelt werden, damit mit i < j für alle Produktionen gilt.

Dadurch erhält man

was eine linksrekursive Ableitung erzeugt. Daher führen wir ein neues Nichtterminalsymbol B₂ ein und wandeln in rechtsrekursive Produktion um

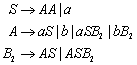
Dann liegen die A-Produktionen schon in Greibach Normalform vor und wir können zum zweiten Schritt übergehen.

2. Schritt

Jetzt muss das erste A der rechten Seite von S durch die A-Produktionen ersetzt werden und man erhält

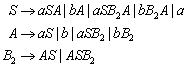
Schön! Jetzt liegen alle Produktion in der gewünschten Form vor, bis auf die B₂-Produktionen, was jedoch auch leicht bewerkstelligt ist.

3. Schritt

Das erste Nichtterminalsymbol der rechten Seite der B₂-Produktionen ist A und wird jeweils durch die beiden A-Produktionen ersetzt, so dass vier neue Produktionen entstehen.

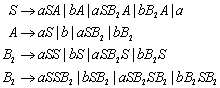
Somit liegen alle Produktionen die Greibach Normalform und die Umwandlung ist abgeschlossen.

20 Vorlesung vom 20. Juni 2000

20.1 Odgens Lemma

Satz:

Sei eine kontextfreie Grammatik. Dann existiert eine Konstante (welche im Allgemeinen recht groß ist), so dass für alle Wörter der Sprache mit und , in denen mindestens Positionen markiert sind, gilt:

Das Wort kann geschrieben werden, als die Zerlegung mit den folgenden 4 Bedingungen:

1. enthält mindestens eine markierte Position,

2. und enthalten beide markierte Positionen, oder aber und enthalten beide markierte Positionen,

3. enthält höchstens markiere Positionen

4. Es existiert ein Nichtterminal mit:

Abbildung 37

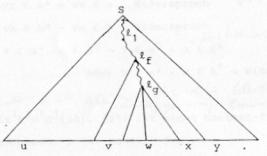
Das Bild zeigt, wie man sich dieses am besten vorstellen kann. Es gilt einen Weg vom Startsymbol aus hin zu den markierten Blättern zu finden. Da nun der Weg sehr lang ist, existiert eine Schliefe. Man betrachtet dann den Teilbaum der letzten Wiederholung. Man sieht nun, dass zumindest eine markierte Position enthalten muss.

Beweis des Satzes:

Es gelte:

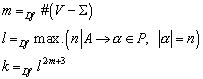
Es sei dann mit und weiterhin mindestens Positionen in markiert. Schließlich sei der Ableitungsbaum für mit der Länge . Ein Knoten heißt Verzweigungsknoten, wenn mindestens zwei direkte Nachfolger hat. Ein Beispiel wäre, wenn der Knoten zwei Nachfolger und hat, welche beide markierte Blätter unter ihren Nachfolgern haben.

Nun lässt sich ein Weg durch den Ableitungsbaum wie folgt konstruieren:

1. ist die Wurzel von ,

2. betrachtet man die Nachfolger eines Knoten . Sollte nur einer von ’s direkten Nachfolgern markierte Knoten haben, so wird dieser der Nachfolger .

3. Wenn ein Verzweigungsknoten ist, dann soll derjenige direkte Nachfolger sein, der die größte Zahl von markierten Blättern als Nachfolger hat. Bei Gleichheit kann beliebig gewählt werden.

4. Wenn ein Blatt ist, endet die Konstruktion.

Nun ist der Weg.

Behauptung:

Wenn der Weg Verzweigungsknoten enthält, dann hat markierte Blätter. Der Beweis folgt durch Induktion. Für gilt:

markierte Blätter. Angenommen, die Aussage ist richtig für . Wenn kein Verzweigungsknoten ist, dann haben und dieselbe Anzahl von markierten Blättern. Wenn ein Verzweigungsknoten ist, dann hat mindestens viele markierte Blätter bei Verzweigungsknoten.

In muss es mindestens viele Verzweigungsknoten geben. Denn anderenfalls hätte viele markierte Blätter. Das wäre jedoch ein Widerspruch, denn ist ein Blatt, und somit kein Verzweigungsknoten. Es gilt also .

Seien nun die letzten Verzweigungsknoten. heißt „linker Verzweigungsknoten“, wenn ein linker direkter Nachfolger von , der nicht auf dem Weg liegt, ein markiertes Blatt links von enthält. Analog dazu ist der „rechte Verzweigungsknoten“, wenn ein rechter direkter Nachfolger von , der nicht auf dem Weg liegt, ein markiertes Blatt rechts von enthält.

Ohne Beschränkung der Allgemeinheit gilt: Es gibt mindestens viele linke Verzweigungsknoten. Seien nun die letzten linken Verzweigungsknoten in . Unter gibt es dann zwei Knoten und mit der selben Bezeichnung, da . Für den Fall, dass echt kleiner als ist, sieht dies wie auf dem folgenden Bild aus:

Abbildung 38

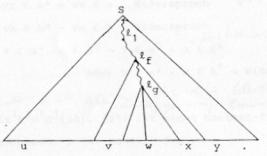
Man kann nun nennen. Es ergibt sich dann:

Und damit gilt dann:

Da nun ein linker Verzweigungsknoten ist, hat mindestens ein markiertes Blatt. Des weiteren ist ein linker Verzweigungsknoten und damit hat mindestens ein markiertes Blatt. enthält als markiertes Blatt .

Es gilt auch, dass der -te Verzweigungsknoten vom ende ist. Somit hat höchstens viele markierte Blätter. Da ein Nachfolger von ist, hat höchstens markierte Blätter.

Analog zu dem eben vorgeführten Beweis für linke Verzweigungsknoten, läuft auch der Fall für rechte Verzweigungsknoten. Hier enthalten dann und jeweils mindestens ein markiertes Blatt.

Korollar: (Pumping Lemma nach Bar-Hillel, Perles, Shamir)

Sei eine kontextfreie Sprache. Dann existiert eine Konstante in der Art, dass, wenn und ist, dann gilt:

Es existiert für eine Zerlegung in mit und:

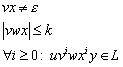
Zum Beweis dieses Korollars, wählt man eine beliebige kontextfreie Grammatik für und markiert alle Positionen in

20.1.1 Beispiele für Kontextfreiheit und Nichtkontextfreiheit

Behauptung:

Die Sprache ist nicht kontextfrei.

Beweis:

Angenommen die Sprache wäre kontextfrei. Es sei dann die Konstante des Pumping Lemmas. Und es gilt:

Es existiert dann eine Zerlegung für mit:

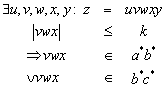
Es soll hier nur der Fall betrachtet werden. Dafür gilt:

Nun gibt es drei Fälle zu beachten:

1. dies stellt aber einen Widerspruch dar, denn die Anzahl der a’s würde schneller wachsen.

2. und wieder haben wir einen Widerspruch, da hie die b’s zu schnell wachsen, schließlich bleibt noch

3. auch in diesem Fall bekommt man einen Widerspruch, denn die c’s bleiben auf der Strecke.

Behauptung:

Die Sprache ist nicht kontextfrei.

Beweis:

Angenommen, die Sprache wäre kontextfrei. Es sei nun die Konstante des Pumping Lemmas. Dann gibt es eine Zerlegung von in mit und .

Wie man sieht, gilt:

1. enthält höchstens zwei verschiedene Symbole,

2. Falls zwei verschiedene Symbole enthält, müssen diese „benachbart“ sein. Dann erhält man durch „pumpen“:

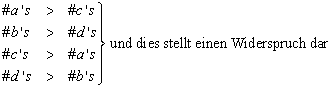
Man erhält also jedes Mal einen Widerspruch, da es nicht zu schaffen ist eine gleiche Anzahl von a’s und c’s oder b’s und d’s zu erreichen.

Behauptung:

Die Sprache ist nicht kontextfrei.

Beweis:

Angenommen die Sprache wäre kontextfrei. Sei nun die Odgens Konstante. Dann gibt es für ein Wort der Sprache eine Zerlegung . Es seien nun alle a’s markiert.

1. und enthalten a’s.

Dann gilt: und damit gilt für . Es gibt dann die folgenden 3 Fälle:

Dann gilt: und somit mit . Dann sollte das Wort: in der Sprache sein, dies kann jedoch nicht sein, da die Anzahl der a’s gleich der Anzahl der b’s.

Dann ist mit und somit müsste das Wort: in der Sprache sein. Jedoch führt auch dies zu einem Widerspruch, da die Anzahl der a’s gleich der Anzahl der c’s ist. Bleibt noch ein Fall zu behandeln.

hier ist für . Dann müsste das Wort: in der Sprache sein. Jedoch ist hier die Anzahl der a’s so groß wie die Anzahl der b’s, was einen Widerspruch darstellt.

2. Der Fall, dass und beide a’s enthalten, funktioniert analog zum 1. Fall. Somit soll es hier nicht wiederholt werden.

Behauptung:

Die Sprache ist eine kontextfreie Sprache, die inhärent mehrdeutig ist.

Beweis:

Zuerst soll noch mal wiederholt werden, was inhärent mehrdeutig bedeutet. Dies bedeutet, dass egal welche Ableitung gewählt wird, immer 2 mögliche Wege existieren.

Um dies zu zeigen, genügt es eine kontextfreie Grammatik aufzustellen, welche mehrdeutig ist. Eine solche kontextfreie Grammatik ist:

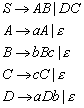
Diese Grammatik ist mehrdeutig, wie man schnell an folgendem Beispiel erkennt:

eine andere Ableitung für dieses Wort ist:

wir behaupten, dass jede kontextfreie Grammatik für mehrdeutig sein muss. Sei eine beliebige Grammatik, die erzeugt. Sei weiterhin die Konstante des Odgens Lemma. Es sei nun ohne Einschränkung . Sei . Nun seien alle a’s markiert und . Nach Odgens Lemma gibt es dann für eine Zerlegung für . Dann gilt:

1. enthält mindestens ein a.

3. . Hierbei gilt, dass mit Sicherheit nicht zwei verschiedene Symbole enthalten kann, denn sonst würde durch das Pumpen „gemischte“ Folgen erzeugt werden.

4. enthält höchstens viele a’s.

Nun sind die folgenden Fälle zu betrachten::

Dann gilt: und damit für und man erhält Wörter: die auch aus der Sprache stammen müssten. Jedoch stellt dieses einen Widerspruch dar, da weder die Anzahl von a’s und b’s, noch die Anzahl der b’s und c’s gleich ist.

Es ist dann mit und es gilt für . Damit bekommt man Wörter: , die auch in der Sprache sein müssen. Doch wie schon bei a) bekommt man einen Widerspruch.

Es gilt: für und weiterhin für . Damit bekommt man die folgenden Wörter:, die Element der Sprache sein müssen. Es gilt also zwei weitere Fälle zu unterscheiden zum einen den Fall und zum anderen :

Damit würden Wörter: diese müssten in der Sprache sein, jedoch ist dies ein Widerspruch.

Es gilt damit: . Für gilt dann:

Eine ähnliche Argumentation liefert dann für den umgekehrten Fall: . Für mit und mit . Schließlich kommt man zu der Ableitung:

Behauptung:

Diese beiden Ableitungen repräsentieren verschiedene Ableitungsbäume.

Beweis:

Angenommen, diese beiden Ableitungen beschreiben denselben Ableitungsbaum.

erzeuge a’s und b’s während, b’s und c’s erzeugt. Somit ist kein Nachfolger von und ist kein Nachfolger von . Betrachtet man nun die Ableitung:

mit

Nun muss für alle gelten:

Nun ist hinreichend groß zu wählen.

Es gilt und . Damit ist also . Somit erhält man also mit . Dies ist jedoch ein Widerspruch, da wir entweder eine gleiche Anzahl von a’s und b’s wollten, oder aber eine gleiche Anzahl von b’s und c’s. Somit können die beiden Ableitungen nicht den selben Ableitungsbaum beschrieben haben.

21 Vorlesung vom 27. Juni 2000

21.1 Deterministische PDA

Wir betrachten nun eine Sprachklasse, die echt zwischen den regulären Mengen und den kontextfreien Sprachen liegen: die deterministischen kontextfreien Sprachen (DCFL). Diese sind interessant, da es sich herausstellt, dass die Syntax vieler Programmiersprachen mittels DCFLs beschrieben werden kann.

Definition:

Sei ein PDA. M heißt dann deterministisch (DPDA):

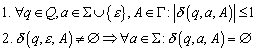
Regel 1 verhindert Wahlmöglichkeiten für dieselbe Eingabe. Regel 2 verhindert die Wahl zwischen der Benutzung eines Eingabesymbols und einer e-Bewegung.

Definition:

Eine Sprache heißt deterministisch kontextfrei (dkfS): Es existiert ein DPDA mit L = T(M).

21.1.1 Beispiele

· Die Sprache ist deterministisch.

· Die Sprache ist nicht deterministisch.

Beim letzten Beispiel müsste der Automat raten, ob für ein a nun ein oder zwei b vorliegen müssen.

Dagegen gilt:

· ist deterministisch, falls gilt d₁ ¹ d₂.

· ist deterministisch, falls gilt d₁ ¹ d₂. Dabei wird so vorgegangen: zunächst werden für jedes a zwei Symbole auf den Keller gelegt. Wenn d₁ gelesen wird, so wird je ein Symbol wieder vom Keller gelöscht, ansonsten wird mit den je zweiten weitergearbeitet.

· ist nicht deterministisch.

21.1.2 kfS und dkfS

Satz:

Sei L eine kontextfreie Sprache (kfS). Dann gibt es eine deterministische kontextfreie Sprache L‘ (dkfS) und einen Homomorphismus h mit h(L‘) = L.

Beweis:

Sei L kontextfrei. Daraus folgt, dass es einen PDA geben muss mit L = T(M).

Es sei

Also ist m die maximale Länge von Symbolen, die auf den Keller gestellt werden. Es sei weiter

mit .

Wir definieren nun den deterministischen PDA M‘ wie folgt:

mit

Wir müssen durch Induktion den Determinismus zeigen:

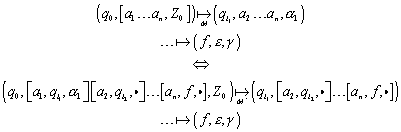
Abbildung 39 - Beispiel zum Beweis

In Abbildung 39 sieht man das Prinzip des Beweises. Oben sieht man einen nichtdeterministischen Kellerautomaten (da bei der gleichen Eingabe in zwei verschiedene Zustände p, r gewechselt werden kann).

Im unteren Teil der Abbildung sieht man nun den deterministischen Automaten mit den neuen Eingabesymbolen [a,a,p] und [a,b,r]. Es wird also eine Alphabetvergrößerung vorgenommen. Um diese Zeichen wieder auf die alten Zeichen zurückzumappen wird der folgende Homomorphismus definiert:

Somit gilt .

21.2 Turing-Maschinen und Entscheidbarkeit

21.2.1 Problem, Algorithmus, Entscheidbarkeit

Definition (Problem):

Ein Problem ist ein Paar mit

c ist also letztendlich die Beschreibung des Problems, das wir lösen wollen.

Definition (Algorithmus):

Ein Algorithmus A für ein Problem ist eine endliche Menge von Instruktionen, die für alle hält mit

Definition (Entscheidbarkeit):

Ein Problem heißt entscheidbar

Beispiel 1

Das Problem mit

Beispiel 2

Das Problem (Leerheitsproblem) mit

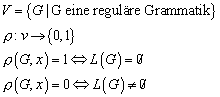
21.2.2 Modelle für Algorithmen

Es gibt unter anderem die folgenden beiden Modelle für Algorithmen:

· Turing Maschinen (Alan Turing)

· Rekursive Funktionen (Kurt Gödel)

Diese beiden Ansätze sind jedoch äquivalent.

21.2.3 Churchsche These

Ende endliche Menge A von Instruktionen ist ein Algorithmus genau dann, wenn eine Turing-Maschine m existiert mit:

21.2.4 Turing-Maschine

Definition (Turing-Maschine):

Eine Turing-Maschine M ist ein 7-Tupel mit

Dabei ist zu beachten, dass {L, R} die Bewegungen des Schreib-/Lesekopfes darstellen sollen. d ist in der Regel partiell, d. h. nicht überall definiert.

Eine Turingmaschine kann man sich also vorstellen als eine Maschine, die auf einem (Eingabe)band operiert. Sie kann dabei ein Zeichen lesen und abhängig von diesem und dem momentanen Zustand, in dem sie sich befindet, ein neues Zeichen an die Stelle des Gelesenen schreiben, in einen neuen Zustand wechseln und den Schreib-/Lesekopf nach recht oder links um eine Stelle bewegen.

Definition (Konfiguration):

Sei eine Turing-Maschine. Eine Konfiguration von M wird wie folgt bezeichnet:

Dabei gilt , so dass a₁ das am weitesten links stehende Nicht-Blank-Symbol und a₂ das am weitesten rechts stehende Nicht-Blank-Symbol enthält. q ist der gegenwärtige Zustand der Maschine und kennzeichnet auch die Position des Schreib-/Lesekopfes.

Wir können die Bewegung einer Turing-Maschine wie folgt formal beschreiben. Zunächst die Linksbewegung:

Hierbei wird vom Zustand q aus das aktuelle Zeichen (X_i) ersetzt durch Y, in den Zustand p verzweigt und der Kopf eine Stelle nach links bewegt.

Analog die Rechtsbewegung:

Wir bezeichnen mit und die üblichen Erweiterungen.

Es ist

die Menge der von M akzeptierten Eingabewörter.

Wir vereinbaren, dass M in einem akzeptierenden Zustand f Î F stets anhält.

Beispiel

Wir betrachten eine Turing-Maschine für die Sprache .

Es sind .

Die Übergangsfunktion d geben wir in folgender Tabelle an:

q₀0	q₁XR	erste 0 von links durch X ersetzen
q₁0 q₁Y q₁1	q₁0R q₁YR q₂YL	zur ersten 1 nach rechts gehen durch Y ersetzen
q₂Y q₂X q₂0	q₂YL q₃XR q₄0L	nach links die erste 0 suchen falls keine mehr da: in q₃ gehen
q₄0 q₄X	q₄0L q₀XR	nach links das erste X suchen
q₃Y q₃B	q₃YR q₅YR	keine Nullen mehr da Þ prüfen, ob auch keine Einsen mehr da sind. Falls ja: in akzeptierenden Zustand gehen!

21.2.5 Universelle Turingmaschine

Wir wollen nun eine Turing-Maschine bauen, die andere Turingmaschinen simulieren kann – und zwar auf jedes Eingabewort hin. Wir wollen also eine Turing-Maschine U mit folgender Eigenschaft:

· M sei eine beliebige Turingmaschine

· x sei ein beliebiges Eingabewort

· Dann führt U bei Eingabe von (M,x) die Simulation von M auf x durch.

Jetzt ist aber die Frage, wie die Eingabe (M,x) aussehen soll. Hierfür müssen wir eine Kodierung auf dem Band vornehmen.

Wir stellen zunächst folgendes fest:

Zu jedem Alphabet G - {B} gibt es eine Kodierung in {0,1}^*, so dass gilt

Wir nehmen also im weiteren an, dass alle Turing-Maschinen auf einem Alphabet {0,1,B} mit S = {0,1} arbeiten. Wir wollen nun die zu simulierende Turing-Maschine selbst kodieren. Wir wählen hierfür das Alphabet

Dabei ist

· c ein Trennzeichen für verschiedene Blöcke unserer Codierung

· 1 verwenden wir zur Darstellung der Zustände

· 0 verwenden wir, wenn d an einer Stelle nicht definiert ist

· L, R sind die Kopfbewegungen

Wir verwenden folgendes Schema:

ccc

ccc

Block für

Eingabe „B“

„0“

„B“

„0“

„1“

Dabei gilt folgendes:

1. ccc bezeichnet die Randmarkierung

2. c bezeichnet die Eingabesymbolblockmarkierung

3. cc bezeichnet die Zustandsblockmarkierung

Jeder Zustand erhält einen Zustandsblock. In jedem Zustandsblock gibt es je einen Eingabesymbolblock für die drei möglichen Eingabesymbole B, 0 , 1. Ein Eingabesymbolblock sieht beispielhaft so aus:

c111L1c

Dies bedeutet, dass in den Zustand 3 (111) gegangen, der Kopf nach links bewegt und an die aktuelle Position eine 1 geschrieben werden soll.

Beispiel:

Wir wollen die Kodierung folgender Übergangstabelle haben:

q₁1	q₂0R
q₂B	q₃1L
q₂0	q₃1L
q₂1	q₂1R
q₃B	q₄0R
q₃0	q₄0R
q₃1	q₃1L

Nach dem obigen Schema lautet die Kodierung:

ccc	0c0c11R0	cc	111L1c111L1c11R1	cc	1111R0c1111R0c111L1	cc	0c0c0	ccc
	q₁		q₂		q₃		q₄

21.2.6 Arbeitsweise der universellen Turing-Maschine

Bei der Arbeit benutzt die virtuelle Turing-Maschine zwei zusätzliche Symbole m₁, m₂ zur Markierung. Dabei markiert m₁ den aktuellen Zustandsblock auf dem Eingabeband (auf dem „cc“) und m₂ das aktuelle Eingabezeichen.

Das Band sieht zu Beginn wie folgt aus (mit Markierung von m₁, m₂):

	m₁		m₂
ccc	...	ccc	Kod(x)

Die Vorgehensweise ist nun die folgende:

1. U sucht m2 und merkt sich das dort gefundene Symbol, z. B. A Î {B,0,1}

2. U sucht im aktuellen Zustandsblock (Merker: m1) die zugehörige Anweisung für A

3. U merkt sich, wodurch A zu ersetzen ist und ob nach rechts oder links gegangen wird

4. U versetzt m1 an den Anfang des Zustandsblocks, der als Nachfolgezustand angegeben wird (Subroutine)

5. U geht zu m2, ändert A und versetzt m2 nach links oder nach rechts

6. Gehe nach 1

Diese Vorgehensweise kann natürlich auch formalisiert werden.

Insgesamt folgt aber

In diesem Ablauf haben wir die akzeptierenden Zustände von M nicht betrachtet. Man kann sich aber leicht vorstellen, dass jede Turingmaschine mit mehreren akzeptierenden Zuständen in eine äquivalente Turingmaschine mit nur einem akzeptierenden Zustand umgewandelt werden kann (indem man einfach einen neuen Zustand einführt und alle akzeptierenden Zustände auf diesen verweist). Dann kann die universelle Turingmaschine durch eine geeignete Erweiterung der Kodierung von M leicht feststellen, ob diese in einem akzeptierenden Zustand ist.

21.2.7 Halteproblem für Turing-Maschinen

Wir formulieren das Halteproblem:

Gibt es einen Algorithmus (Turing-Maschine), der für beliebige Paare (M, x), wobei M eine Turing-Maschine und x ein Wort sei, entscheidet, ob M auf x hält?

Wir kodieren wieder, diesmal jedoch alle Turing-Maschinen in einem endlichen Alphabet und alle Eingabewerte in {0,1}^*. In beiden Kodierungen existiert eine lineare (lexikographische Ordnung).

Wir beweisen zunächst einen Hilfssatz:

Lemma:

Sei die Sprache der Wörter mit der Nummer i, die nicht von der i-ten Turing-Maschine akzeptiert werden. Zu dieser Sprache existiert keine Turingmaschine mit T(M) = L₁.

Beweis:

Angenommen, es gäbe eine solche Turingmaschine M mit L₁ = T(M). Daraus folgt automatisch

(weil M ja selbst eine Turingmaschine ist und sie daher eine Nummer j besitzen muss). Dann aber gilt

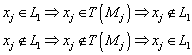
Beide Fälle sind Widersprüche, so dass die Annahme falsch gewesen sein muss.

Satz (Halteproblem):

Es gibt keinen Algorithmus (Turing-Maschine), der für ein beliebiges Paar (M,x), wobei M eine Turing-Maschine und x ein Wort sei, entscheidet, ob M auf x hält.

Beweis:

Wir nehmen an, dass ein solcher Algorithmus A existiert:

Wir behaupten, dass von einer Turing-Maschine akzeptierbar ist. U sei die universelle Turing-Maschine.

Wir konstruieren jetzt eine Turing-Maschine M:

1. Eingabe ist x

2. Durch sukzessives Iterieren der Worte x₁,x₂,...,x_n bestimmen wir das i mit x_i = x. (Wir bestimmen also die Nummer des Wortes x)

3. Durch sukzessives Iterieren erzeugen wir über dem Kodierungsalphabet die Turing-Maschine M_i.

4. Jetzt wenden wir A (M_i,x_i) an.

5. Wenn A (M_i,x_i) = 0 Þ M akzeptiert x_i.

6. Wenn A (M_i,x_i) = 1 Þ M akzeptiert nicht x_i

7. Mi akzeptiert nicht x_i Þ M akzeptiert x_i

Daraus folgt: . Das ist aber ein Widerspruch zum obigen Lemma. Damit folgt ein Widerspruch zur Annahme und die gewünschte Turing-Maschine kann nicht existieren.

21.2.8 Rekursive Mengen

Definition (rekursive Menge):

Eine Menge S heißt „rekursiv“ Û Es existiert eine Turing-Maschine M, die auf allen Eingaben aus S^* hält, mit S = T(M). Wichtig ist hierbei die Aussage „auf allen Eingaben“. Bildlich kann man sich die Definition wie in Abbildung 40 vorstellen.

Defintion (rekursiv aufzählbar):

Eine Menge heißt „rekursiv aufzählbar“ :Û Es existiert eine Turing-Maschine M mit S = T(M).

Diese Situation ist in Abbildung 41 dargestellt.

Satz:

Eine Menge ist rekursiv ist rekursiv.

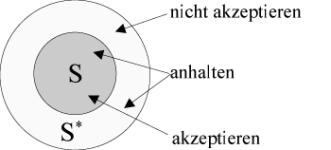
Abbildung 40 - Rekursive Mengen

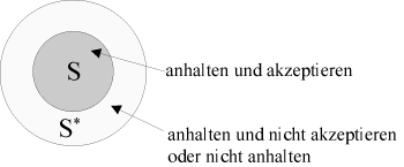
Abbildung 41 - Rekursiv aufzählbare Mengen

Beweis:

L ist rekursiv. Daraus folgt, dass es eine Turing-Maschine gibt mit

· L = T(M)

Sei eine neue Turingmaschine, die M simuliere. Wir haben .

Es gelte nun

Die Maschine M₁ hält immer!

Weiter gilt .

Damit ist auch rekursiv. Die umgekehrte Richtung zeigt man analog.

Satz:

Es gibt eine rekursiv aufzählbare Menge, deren Komplement nicht rekursiv aufzählbar ist.

Beweis:

Es sei . Weiter sei U die modifizierte universelle Turingmaschine[15]. Dann gilt:

22 Literaturverzeichnis

1. Uwe Schöning: "Theoretische Informatik - kurzgefaßt", 3. Auflage, 1997

2. Spektrum Akademischer Verlag GmbH Heidelberg, Berlin

3. Skript „Theoretische Informatik II“, Prof. Dr. Wotschke Universität Frankfurt

4. Vorlesung „Theoretische Informatik II“, Prof. Dr. Wotschke Universität Frankfurt

5. Skript „Theoretische Informatik II“, Prof. Dr. Schnittger Universität Frankfurt

6. J. E. Hopcroft und J. D. Ullman: "Einführung in die Automatentheorie, formale Sprachen und Komplexitätstheorie", Addison-Wesley, 3. Auflage, 1996

7. "Schülerduden: Informatik", Dudenverlag, 3. Auflage, 1997

8. "Schülerduden: Die Mathematik II", Dudenverlag, 3. Auflage, 1991

23 Abbildungsverzeichnis

Abbildung 1 - Grafische Zuordnung von Mengenelementen. 14

Abbildung 2 - Quadratisch unendliches Schema der Bruchzahlen. 14

Abbildung 3 - Prinzip eines endlichen Automaten. 17

Abbildung 4 - Beispiel eines endlichen Automaten. 18

Abbildung 5 - Beispiel eines endlichen Automaten. 19

Abbildung 6 – Beispiel eines NFA. 25

Abbildung 7 – ein nichtdeterministischer, endlicher Automat M.. 31

Abbildung 8 - Der DFA, der zu' M äquivalent ist31

Abbildung 9: NFA zur Sprache L₄32

Abbildung 10: der aus dem NFA erzeugte DFA für die Sprache L₄32

Abbildung 11: NFA für die Sprache Ln. 33

Abbildung 12 - Homomorphismus. 44

Abbildung 13 - Homomorphismus zwischen Automat M und Nerode Automat45

Abbildung 14: Beispiel eines nicht minimalen Automaten. 52

Abbildung 15 der minimierte Automat M'53

Abbildung 16 – ein Transitionsdiagramm.. 60

Abbildung 17 – die Epsilon-Hülle im Transitionsdiagramm.. 61

Abbildung 18 - Äquivalenzkreislauf reguläre Ausdrücke - endliche Automaten. 64

Abbildung 19 - NFAs für reguläre Ausdrücke ohne Operatoren. 65

Abbildung 20 - Vereinigung von regulären Ausdrücken. 65

Abbildung 21 - Konkatenation von regulären Ausdrücken. 66

Abbildung 22 - Kleensche Hülle über regulärem Ausdruck. 67

Abbildung 23 - Automat für 1*. 68

Abbildung 24 - Automat für 01*. 68

Abbildung 25 - Gesamter Automat69

Abbildung 26: der endliche Automat des Beispiels. 75

Abbildung 27 - Ableitungsbaum einer Produktion. 94

Abbildung 28 - richtige und falsche Ableitungsbäume von e-Produktionen. 94

Abbildung 29 - Beispiel Ableitungsbaum für Wort aabbaa. 95

Abbildung 30 - Ableitung bei einem einzelnen inneren Knoten. 96

Abbildung 31 - Illustration eines A-Baum.. 97

Abbildung 32 - A-Baum mit Kinderknoten und Xj-/Xi-Teilbäumen. 97

Abbildung 33. 108

Abbildung 34. 110

Abbildung 35. 112

Abbildung 36 - Links- und rechtrekursive Ableitungen. 121

Abbildung 37. 126

Abbildung 38. 127

Abbildung 39 - Beispiel zum Beweis. 105

Abbildung 40 - Rekursive Mengen. 110

Abbildung 41 - Rekursiv aufzählbare Mengen. 111

24 Index

[1] Vgl.: INTRODUCTION TO AUTOMATA THEORY, LANGUAGES AND COMPUTATION by John E. HOPECROFT and Jeffrey D. ULLMAN pages 22f

[2] Ein DFA ist ein Spezialfall des NFA, bei dem es für jeden Zustand eine einzigartige Übergangsfunktion für jedes Symbol gibt.

[3] Bei der homomorphen Eigenschaft handelt es sich nicht um eine zwangsläufige Konsequenz, oder um eine durch das Monoid definierten Eigenschaft. Vielmehr wird der Homomorphismus (willkürlich) gefordert, um die neue, algebraische Struktur als „Ring“ zu erhalten

[4] ist zwar beweisbar, an dieser Stelle verzichten wir aber darauf.

[6] Ein NFA wird ja schon dadurch zum e-NFA, dass man von jedem Zustand einen mit „e“ markierten Pfeil auf sich selber einzeichnet. Dadurch verändert sich das Verhalten des Automaten nicht.

[7] Hier wird die Induktionsannahme für Länge(x)=1 verwendet. Da in dem aktuellen Induktionsschritt Wörter der Länge > 1 betrachtet werden, ist dieses Vorgehen erlaubt.

[8] Besuchen bezeichnet hier in den Zustand einzutreten und wieder herauszutreten

[9] Für die Korrektheit übernehme ich keine Haftung ;-)

[10] Die Begriffe „starten“ und „enden“ dürfen in diesem Zusammenhang auch vertauscht werden.

[11] Dieser, ausgezeichnete Zustand f ist das wichtigste Element der Menge der akzeptierenden Zustände...

[12] Dieser Beweis wurde im Skript komplett weggelassen. Warum, ist mir nicht klar.

[13] Man kann bei einem PDA natürlich nicht von „Terminalen“ und „Nichtterminalen“ sprechen. Diese Bezeichnungen beruhen auf der Bedeutung der jeweiligen Symbole in Bezug auf die kontextfreie Grammatik, die dem PDA zugrunde liegt.

[14] Dieses Vorgehen ist an sich beweistechnisch nicht korrekt.

[15] Modifiziert heißt hier: die i-te Turingmaschine muss erst wie in Abschnitt 21.2.7 beschrieben konstruiert werden.